Question

Obtain the equation of frequency of stationary waves produced in an open pipe and show that all harmonics are possible in it.

Answer 1

Hint When air passes through an open pipe, it also causes the pipe to oscillate with it. This oscillation only happens for certain frequencies of the vibrating air. Stationary waves are formed when the frequency and the length of the column are such that the waves appear to be stationary. They consist of points of no movement, node, and points of maximum movement, antinode.

Complete Step by step solution
Let there be an open pipe of length L.
Suppose, a wave passes through this pipe. The wavelength of this wave is $\lambda$while the frequency of this wave is $f$. The relationship between these quantities is given by,
$v = \lambda f$, where v is the velocity of propagation of wave.

To create a standing wave, the wave must oscillate in such a way that the wave doesn’t move forward or backward inside the pipe. Such a formation would look like-

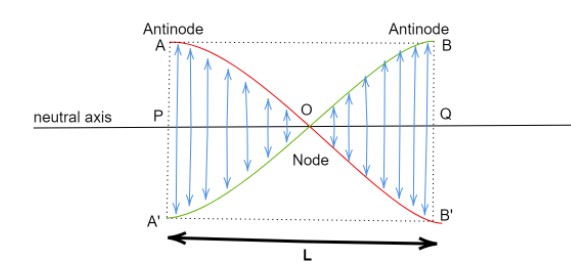
This is the minimum wavelength at which standing waves are possible. We can see that the wavelength of the wave required to form the first standing wave or the fundamental frequency stretches two times the total length of the column, or
${\lambda _1} = 2L$
Where L is the length of the column and ${\lambda _1}$is the first wavelength or the first harmonic. The corresponding frequency, known as the “fundamental frequency” is given by-
${f_1} = \dfrac{v}{{2L}}$
A harmonic contains places that have either most up and down displacement (amplitude), known as Antinodes, and places with no displacement at all called the Nodes.
First harmonic has 1 Node and 2 antinodes.
The next wavelength at which standing waves are possible is at,
${\lambda _2} = L$
Thus the frequency,
${f_2} = \dfrac{v}{L}$or ${f_2} = \dfrac{{2v}}{{2L}}$
This is the second harmonic.
It contains 2 nodes and 3 antinodes.
For the third harmonic the number of nodes would be 3 and the number of antinodes would be 4.
${\lambda _3} = \dfrac{v}{{{f_3}}} = \dfrac{{2L}}{3}$ or ${f_3} = \dfrac{{3v}}{{2L}}$
We can see a relationship between the wavelength or frequency of these standing waves with the length of the column-
${\lambda _n} = \dfrac{v}{{{f_n}}} = \dfrac{{2L}}{n}$
Where, n follows the series of natural number, $n = 1,2,3,4,5...$
$n$is known as the number of harmonics. For example, $n = 5$is known as the fifth harmonic, and the frequency corresponding to it is,
${f_5} = \dfrac{{5v}}{{2L}}$
The number of nodes(N) for a harmonic is given by-
$N = n$

The number of antinodes (A) for a harmonic is given by-
$A = n + 1$

Note When air is passed through an open pipe, the sound produced by it will correspond to its first harmonic of fundamental frequency. The other harmonics, known as overtones, are also produced but their amplitude is much less than the first harmonic. These harmonics are also known as overtone. Therefore, $2nd$harmonic is$1st$overtone, $3rd$harmonic is$2nd$overtone, etc. In general,
$Overtone = harmonic - 1$