Question
Question: Obtain the capacitance of the five capacitors which are connected to a \(100V\) supply. Calculate th...
Obtain the capacitance of the five capacitors which are connected to a 100V supply. Calculate the total charge and total energy stored in the network.
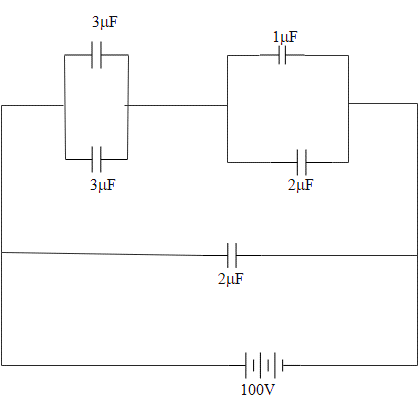
Solution
First of all find the equivalent capacitance of the network shown. The energy stored will be the half of the product of the equivalent capacitance and the square of the potential. This information will help you in solving the question.
Complete answer:
First of all let us calculate the equivalent capacitance of the network. The two capacitors having the capacitance 3μF are connected in parallel. Their total capacitance will be,
C1=3+3=6μF
The capacitors having capacitance 1μF and 2μF are parallel. Their total capacitance will be given as,
C2=1+2=3μF
This two total capacitance, C1 and C2 will be in series,
Therefore we can write that,
C12=6+36×3=2μF
This C12will be in parallel to the 2μF capacitor.
Therefore the equivalent capacitance of the network will be,
C=C12+2μF=2+2=4μF
The net capacitance has been obtained.
The energy store in the capacitor will be the half of the product of the equivalent capacitance and the square of the potential. That is we can write the equation as,
U=21CV2
The potential is given by the equation,
V=100V
Substituting the values in it will give,
U=21×4×10−6×(100)2=0.02J
The total charge in the capacitor is given as,
q=CV
Substituting the values in it will give,
q=CV=(4×10−4)×100=4×10−4C
Note:
The energy stored in a capacitor is defined as the work needed to charge the capacitor with no charge on its plates. The energy has been stored in the electrical field in the space in between the plates of the capacitor. It is dependable on the measure of electrical charges on the plates and on the potential difference between the plates.
