Question

Obtain an expression for the period of a simple pendulum. On what factors does it depend on?

Answer 1

To derive the time period of a simple pendulum. We first find all the forces acting on the pendulum for the oscillation to take place. From the force formula we find an equation for acceleration. Comparing this equation with the acceleration equation in simple harmonic motion we find the time period.

Complete step by step solution:
The free body diagram of a simple pendulum is as given below

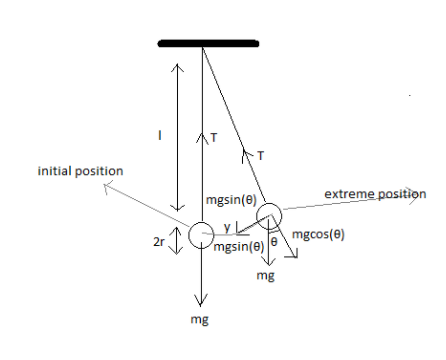
The tension force is represented by $T$
Weight of the bob is represented by$mg$
Gravity is represented by $g$
Mass of bob is represented by $m$
The horizontal component of weight is represented by
$mgsin\theta$
Vertical component of weight is represented by
$mgcos\theta$
Angle $\theta$ is the angle made by the initial position with the extreme position. This is also equal to the angle between weight and its horizontal component from internal angles.
At the initial position there are no components for the weight of Bob. At the extreme position the weight of the Bob is divided into vertical and horizontal components as in the diagram. The tension force and the vertical component of the weight cancel each other.
And the remaining force acting on the pendulum to cause oscillation is
$- mgsin\theta$
Negative sign represented the direction.
Let us take the length of the pendulum as $l$
Radius of Bob as $r$
Total length is represented by $t = r + l$
Taking the diagram as a right angled triangle
$sin\theta$ From the diagram is $\dfrac{y}{l}$
Where $y$ is the displacement of bob
Now the force $- mgsin\theta$ becomes
$\Rightarrow$ $- mg\dfrac{y}{l} = F$
Acceleration is equal to
$\Rightarrow$ $F = ma$
$a = \dfrac{F}{m} = \dfrac{{ - mg\dfrac{y}{l}}}{m} = - g\dfrac{y}{l}$
Taking $\dfrac{g}{l}$ as constant we get
$a = - cy$.....(1)
From shm acceleration is equal to
\Rightarrow$$$a = - {\omega ^2}y$$......(2) Equating (1) and (2) We get \Rightarrow$${\omega ^2} = \dfrac{g}{l}$$\Rightarrow$$\omega $is angular frequency which is equal to$\dfrac{{2\pi }}{T}$Here,$T$represented time period Substituting this in the above equation we get$\Rightarrow$${(\dfrac{{2\pi }}{T})^2} = \dfrac{g}{l}$$\Rightarrow$$\dfrac{{2\pi }}{T} = \sqrt {\dfrac{g}{l}} $$\Rightarrow$$T = 2\pi \sqrt {\dfrac{l}{g}} $Hence time period is$T = 2\pi \sqrt {\dfrac{l}{g}} $
From the final equation we can say that the time period of a pendulum depends on length and acceleration due to gravity.

Note: We can consider the oscillations in a pendulum as simple harmonic motion because if a graph of the displacement of the Bob and the time is drawn it shows a simple harmonic motion. Hence, we can say that an oscillating pendulum is a simple harmonic motion.