Question

Obtain an expression for the maximum speed with which a vehicle can safely negotiate on a curved road banked at angle $\theta$. The coefficient of friction between the wheels and the road will be $\mu$.

Answer 1

The diagram is having a great importance in this question. Find out the relation between the components of the normal force and other forces. Take their ratio to obtain the expression for the angle of banking. These all may help you to solve this question.

Complete step by step answer:
First of all let us draw the diagram for the forces.

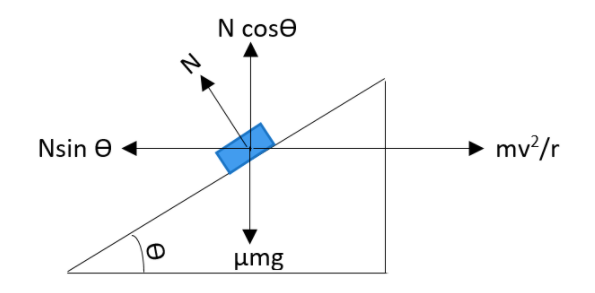
When we observe the figure, we can see the balancing of the forces in it.
The sine component of the normal forces is equivalent to the gravitational force. That is,
$N\sin \theta =\mu mg$
Where $N$be the normal force acting, $\theta$ be the banking angle, $m$ be the mass of the body, $\mu$ be the coefficient of friction and $g$be the acceleration due to gravity.
The cosine component of the normal forces is equivalent to the centripetal force. This can be written as,
$N\cos \theta =m\dfrac{{{v}^{2}}}{r}$
Where $v$ be the velocity of the travel and $r$ be the radius of the path.
Let us take the ratio between them,
$\dfrac{N\sin \theta }{N\cos \theta }=\dfrac{m\dfrac{{{v}^{2}}}{r}}{\mu mg}$
As we all know, the ratio of the sine to the cosine is found to be the tangent of the angle of banking. Therefore we can write that,
$\tan \theta =\dfrac{\dfrac{{{v}^{2}}}{r}}{\mu g}=\dfrac{{{v}^{2}}}{\mu rg}$
Taking the inverse of this will give the angle of banking.
That is,
$\theta ={{\tan }^{-1}}\left( \dfrac{{{v}^{2}}}{\mu rg} \right)$
The maximum speed at which the vehicle can safely drive through the path will be,
$v=\sqrt{\mu rg\tan \theta }$

Note: If the velocity is greater than the maximum safe speed,
$v>\sqrt{\mu rg\tan \theta }$
Then the car sweeps outwards, therefore the radius increases and as a result, the centripetal force decreases and then it balances the sine component of normal force.
If the velocity is less than maximum safe speed,
$v < \sqrt{\mu rg\tan \theta }$
Then the car sweeps inwards, radius gets decreased and hence the centripetal force will increase. This will get balanced by the component of normal force.