Question

Obtain an expression for the magnetic induction at a point due to an infinitely long straight conductor carrying current.

Answer 1

Hint – In this question consider a long straight current carrying conductor, XY let P be any point at some distance a from this point P, consider an element of length dl, so the current passing through it must be idl, consider the angles which the distance between element and the point P is making, then application of Biot-Savart law will help getting the answer.

Complete step-by-step answer:

__

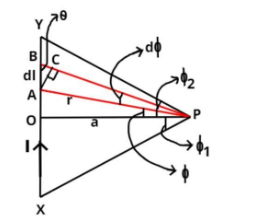
Let XY is an infinitely long straight conductor carrying current I as shown in the figure.
Let, P be a point at a distance (a) from the conductor.
Let AB be a small element of length dl.
Let, $\theta$ be the angle between the current element $Idl$and the line joining the element dl and the point P.
According to Biot-savart law, the magnetic induction at the point P due to the current element $Idl$ is,
$dB = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Idl.\sin \theta }}{{{r^2}}}$..................... (1)
Now let AC be the perpendicular from point A to BP.
Let, $\angle OPA = \phi$, $\angle APB = d\phi$
Now in triangle ABC, sin is the ratio of perpendicular to hypotenuse.
$\Rightarrow \sin \theta = \dfrac{{AC}}{{AB}} = \dfrac{{AC}}{{dl}}$
Therefore, AC = $dl\sin \theta$............... (2)
Now from triangle APC,
$AC = rd\phi$..................... (3), (as angle is very small $\sin d\phi = d\phi$)
From equation (2) and (3) we have,
$\Rightarrow rd\phi = dl\sin \theta$................... (4)
Now substitute equation (4) in equation (1) we have,
$\Rightarrow dB = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Ird\phi }}{{{r^2}}} = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Id\phi }}{r}$.................... (5)
In triangle OPA, $\cos \phi = \dfrac{a}{r}$ (base divided by hypotenuse)
$\Rightarrow r = \dfrac{a}{{\cos \phi }}$....................... (6)
Now substitute the value from equation (6) in equation (5) we have,
$\Rightarrow dB = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Id\phi }}{r} = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Id\phi }}{{\dfrac{a}{{\cos \phi }}}} = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\cos \phi d\phi$
The total magnetic induction at P due to the conductor XY is
$B = \int_{ - {\phi _1}}^{{\phi _2}} {dB}$, ${\phi _1}$ is the angle behind the point P that’s why we take as negative.
Now substitute the value we have,
$\Rightarrow B = \int_{ - {\phi _1}}^{{\phi _2}} {\dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\cos \phi d\phi }$
Now integrate as we know integration of $\cos \phi$ is $\sin \phi$.
$\Rightarrow B = \left[ {\dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\sin \phi } \right]_{ - {\phi _1}}^{{\phi _2}}$
Now apply integration limits we have,
$\Rightarrow B = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\left[ {\sin {\phi _2} - \sin \left( { - {\phi _1}} \right)} \right]$
Now as we know that $\left[ {\sin \left( { - \theta } \right) = - \sin \theta } \right]$ so we have,
$\Rightarrow B = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\left[ {\sin {\phi _2} + \sin {\phi _1}} \right]$
Now for infinitely long conductor, ${\phi _1} = {\phi _2} = {90^o}$
$\Rightarrow B = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\left[ {\sin {{90}^0} + \sin {{90}^0}} \right] = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{I}{a}\left[ {1 + 1} \right] = \dfrac{{{\mu _o}}}{{2\pi }}\dfrac{I}{a}$
So this is the required expression for the magnetic induction at a point due to an infinitely long straight conductor carrying current.

Note – It is advised to remember the direct result for magnetic induction at a point due to infinitely long straight conductor carrying current that is $\dfrac{{{\mu _o}}}{{2\pi }}\dfrac{I}{a}$. This result has direct application in many competitive exams. Biot-Stavart law states that magnetic intensity at any point due to an infinitely long straight wire is directly proportional to the current and is inversely proportional to the distance from the point to the wire.