Question

Obtain an expression for the coefficient of mutual inductance of two long solenoids.

Answer 1

In this question we have been asked to derive an expression for the coefficient of mutual inductance of two long solenoids. Therefore, to solve this question we shall calculate the magnetic field of one solenoid and use the value to calculate the magnetic flux in others. We shall then calculate the coefficient of mutual inductance using these values.

Formula used:
$\phi =BAN$
Where,
$\phi$ is the magnetic flux
B is the magnetic field
A is the area vector
N is the number of turns
$\phi =MI$
Where,
M is the coefficient of mutual inductance
I is the current

Complete step by step solution:
Let ${{S}_{1}}$ and ${{S}_{2}}$ be two long solenoids of length l. the solenoid ${{S}_{2}}$ is wound closely over the solenoid ${{S}_{1}}$as shown in the figure below.

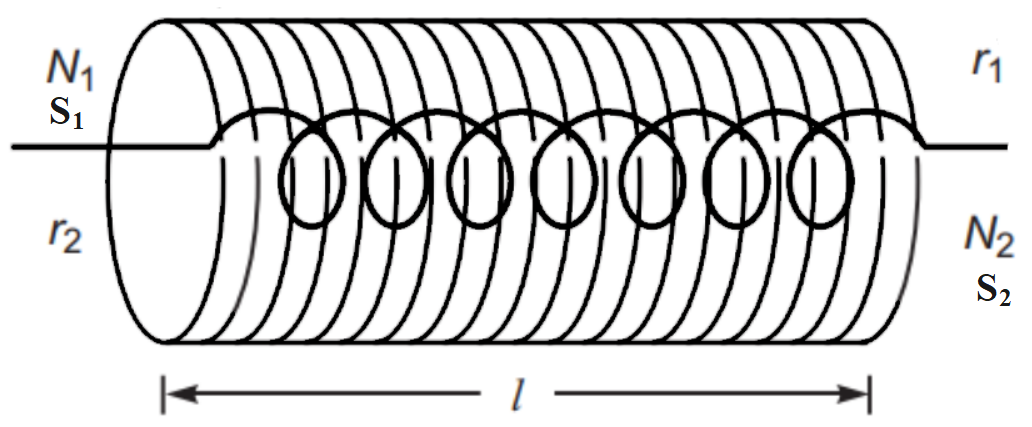
Let N be the number of turns, B be the magnetic field and I be the current in the solenoids
Therefore, we know that magnetic field of solenoid ${{S}_{1}}$ is given by,
${{B}_{1}}={{\mu }_{0}}\dfrac{{{N}_{1}}}{l}{{I}_{1}}$ …………… (1)
The flux linked with solenoid ${{S}_{2}}$ is given by,
${{\phi }_{2}}={{B}_{1}}A{{N}_{2}}$
Therefore, from (1)
We get,
${{\phi }_{2}}=\left( {{\mu }_{0}}\dfrac{{{N}_{1}}}{l}{{I}_{1}} \right)A\times {{N}_{2}}$ ……………….. (2)
But we know that,
${{\phi }_{2}}=M{{I}_{1}}$ ……………… (3)
Where, M is he coefficient of mutual inductance
Therefore, from (2) and (3)
We get,
$M{{I}_{1}}=\dfrac{{{\mu }_{0}}{{N}_{1}}{{N}_{2}}A{{I}_{1}}}{l}$
Therefore,
$M=\dfrac{{{\mu }_{0}}{{N}_{1}}{{N}_{2}}A}{l}$
Therefore, the coefficient of mutual inductance between two given solenoids is $M=\dfrac{{{\mu }_{0}}{{N}_{1}}{{N}_{2}}A}{l}$

Note: When the magnetic field of one coil induces a voltage on another coil, the interaction is known as mutual inductance. Mutual inductance between two cols is defined as the property of the coil due to which it opposes the change of electric current in its counterpart or other coil. The coefficient of mutual inductance is equal to the number of magnetic flux linkage in one coil when current I flows through the second coil.