Question

Obtain an expression for magnetic flux density B at the center of a circular coil of radius R, having N turns and carrying a current $I$.

Answer 1

This problem is based on the application of Biot-savart’s law. This law is used to determine the strength of the magnetic field at any point due to a current-carrying conductor. Biot-savart’s law for the magnetic field obeys inverse square law and the superposition principle.

Complete step by step answer:
Consider a circular coil or a circular loop of radius R, carrying current I. The circular coil consists of a large number of current elements of length $dl$. Let the current element (AB) $Id\vec l$.

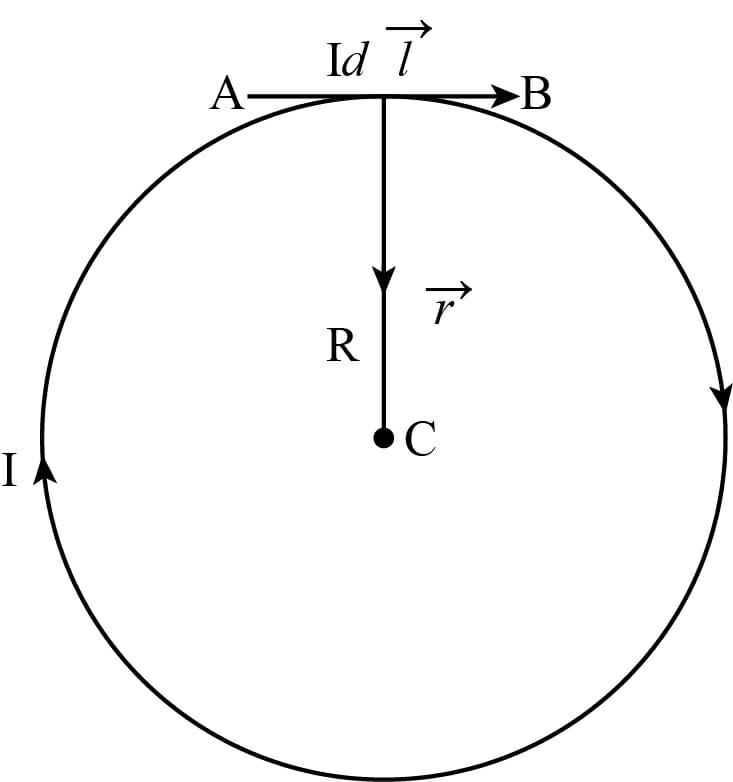
AS per Biot-savart’s law, the magnetic field at point C due to current element AB.
$\Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l \times r}}{{{R^2}}}$
Since the angle between $d\vec l$ and $\hat r$ is $90^\circ$, so
$d\vec l \times \hat r = dl\sin 90^\circ$
$\Rightarrow d\vec l \times \hat r = dl$
Simplifying the above equation, it gives us,
$db = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Idl}}{{{R^2}}}$
Therefore, the magnetic flux at the center of a current-carrying loop
$B = \dfrac{{{\mu _o}I}}{{4\pi }} \times \dfrac{1}{{{R^2}}}\oint {dl}$
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi {R^2}}}2\pi R$
$\Rightarrow B = \left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\dfrac{{2\pi I}}{R}$
However, if the direction of the magnetic field at the center of the current-carrying loop is perpendicular to the plane of the loop and in the upward direction if the current in the loop passes anticlockwise. If a coil has N turns, then the magnetic field at the current coil its center is given by
$\Rightarrow B = \left( {\dfrac{{{\mu _o}}}{{4\pi }}} \right)\dfrac{{N \times 2\pi I}}{R}$
$\Rightarrow B = \dfrac{{{\mu _o}NI}}{{2R}}$

Therefore, An expression for magnetic flux density B at the center of a circular coil of radius R, having N turns and carrying a current $I$ is given by $B = \dfrac{{{\mu _o}NI}}{{2R}}$.

Note:
Here $db$ is the magnetic field, ${\mu _o}$ is the absolute permeability and $dl$ is the small element length. Here the current element is a vector quantity whose magnitude equal to the product of current and length of a small element having a direction to the flow of current i.e. $Id\vec l$.