Question

Obtain an expression for e.m.f induced in a coil rotating with uniform angular velocity in a uniform magnetic field. Show graphically the variation of e.m.f with time(t).
Resistance of a potentiometer wire is $0.1\Omega /cm$. A cell of e.m.f 1.5V is balanced at 300cm on this potentiometer wire. Calculate the current and balancing length for another cell of e.m.f 1.4V on the same potentiometer wire.

Answer 1

For calculating the emf in the coil use the formula $emf=-\dfrac{d\phi }{dt}$. Find the flux through the coil at time t by using $\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$ and differentiate with respect to time.
Use the formula $E=\dfrac{xV}{l}$ and find the potential difference per length and then by Ohm’s law find the current in the circuit. Use the same formula to find the balancing length.

Formula Used:
$emf=-\dfrac{d\phi }{dt}$
$\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$
$\dfrac{d\theta }{dt}=\omega$
$E=\dfrac{xV}{l}$

Complete step-by-step answer :
(i) Consider a circular coil of radius R. Let it be rotating in the vertical plane in a uniform magnetic field (B) with a constant angular velocity $\omega$. Let the direction of the magnetic field be inside the plane of this page. Let the coil rotate from west to east direction.
When the magnetic flux through a coil changes with time, an e.m.f is produced in the coil, which is given as $emf=-\dfrac{d\phi }{dt}$.
At some time t, let the area vector (A) of the coil make an angle $\theta$ with the magnetic field.
Flux through the coil is given as $\phi =\overrightarrow{B}.\overrightarrow{A}=BA\cos \theta$
Therefore, emf produced in the coil is $emf=-\dfrac{d\phi }{dt}=-\dfrac{dBAcos\theta }{dt}$
$\Rightarrow emf=-\dfrac{BAdcos\theta }{dt}=-BA(-\sin \theta )\dfrac{d\theta }{dt}=BA\sin \theta \dfrac{d\theta }{dt}$
Angular velocity is the change in the angle of rotation per unit time. Therefore, $\dfrac{d\theta }{dt}=\omega$
Therefore, $\Rightarrow emf=BA\sin \theta (\omega )=BA\omega \sin \theta$.
The area of the coil is $A=\pi {{R}^{2}}$.
Therefore, $emf=\pi {{R}^{2}}\omega B\sin \theta$…..(i).
Consider $\dfrac{d\theta }{dt}=\omega$
$\Rightarrow d\theta =\omega dt$
Integrate both the sides.
Therefore, we get
$\theta =\omega t+c$.
Let the $\theta =0$ at t=0.
This means that c=0.
$\Rightarrow \theta =\omega t$
Substitute the value of $\theta$ in (i).
$\Rightarrow emf=\pi {{R}^{2}}\omega B\sin \omega t$.
Therefore, the emf produced in the coil is a sinusoidal function of time as shown below.

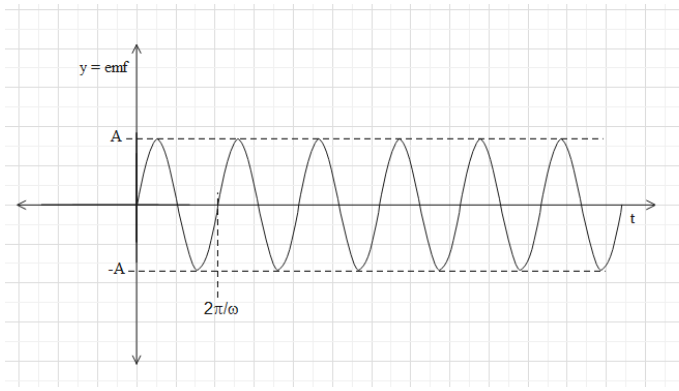
(ii) In a potentiometer, the emf if the cell is given by $E=\dfrac{xV}{l}$, where x is the balancing length and l is the full length of the resistance wire. V is the potential difference across the resistance wire.
In the first case it is given that x=300cm, E=1.5V .
Therefore, $1.5=\dfrac{300V}{l}$
$\Rightarrow \dfrac{V}{l}=\dfrac{1.5}{300}=5\times {{10}^{-3}}Vc{{m}^{-1}}$
This means when the circuit is balanced, the potential difference across 1 cm of the wire is $5\times {{10}^{-3}}V$.
It is given that the resistance of 1 cm length is $0.1\Omega$.
Therefore, the current in the wire is $i=\dfrac{5\times {{10}^{-3}}}{0.1}=5\times {{10}^{-2}}A$
When the cell of 1.4V is connected,
$1.4=\dfrac{xV}{l}$
And $\dfrac{V}{l}=5\times {{10}^{-3}}Vc{{m}^{-1}}$
Therefore, $1.4=x\times 5\times {{10}^{-3}}$
$\Rightarrow x=\dfrac{1.4}{5\times {{10}^{-3}}}=280cm$

Note : (i) In the first solution, keys points to note are the uniform magnetic field and uniform angular velocity of the coil. If these are not constant then the answer will change completely.
(ii) In a potentiometer, the current in the resistance wire is independent of the balancing length. It is the same for all the balancing lengths.