Question

Observe the pattern and fill in the blanks:

1. $2,4,6,8,....$
2. $1,3,6,10,....$
3. 9,109,209,\\_,\\_,\\_

Answer 1

Here, in the given question, we need to observe each pattern and fill in the blanks. In mathematics, the number pattern is a pattern or sequence in a number series. A common relationship between all numbers is generally formed by this pattern. Example: $1,3,5,7,9,....$ these number patterns represent the sequence of odd numbers. Here, we will observe each pattern and fill the blanks using a particular sequence.
There are two common number sequence patterns:
- Arithmetic sequence
- Geometric sequence
The special sequences of number patterns are:
- Square numbers
- Cubic sequence
- Triangular numbers
- Fibonacci numbers

Complete step by step solution:

1. $2,4,6,8,....$
   The given sequence is an arithmetic sequence.
   An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. This difference between consecutive terms is called a common difference.
   $2,4,6,8,....$ is an arithmetic sequence because the difference between consecutive terms is $2$.
   Therefore, our answer will be $2,4,6,8,10,12,14,16$.

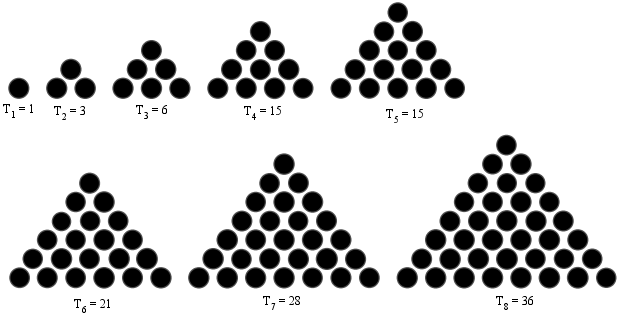
2. $1,3,6,10,....$
   The given sequence is of triangular Numbers.
   A triangular number ${T_n}$ is a figurative number that can be represented in the form of an equilateral triangular grid of elements such that every subsequent row contains an element more than the previous one.
   In the pattern of triangular numbers, the next number in the sequence is added with an extra row.
   First number is $1$.
   In number two, a row is added with two dots to the first number.
   In number three, a row is added with three dots to the second number.
   In number four, a row is added with four dots to the third number and so on
   Therefore, our answer will be $1,3,6,10,15,21,28,36$ 3) 9,109,209,\\_,\\_,\\_
   

3. The given sequence is an arithmetic sequence.
   An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. This difference between consecutive terms is called a common difference.
   9,109,209,\\_,\\_,\\_ is an arithmetic sequence because the difference between consecutive terms is $100$.
   Therefore, our answer will be $9,109,209,309,409,509$.

Note:
We can also solve the patterns by deriving a general formula

1. $2,4,6, 8….$ The $n^{th}$ term in this pattern can also be found by $2n$.
2. $1,3,6,10,....$. The $n^{th}$ term in this pattern can also be found by $\dfrac{n(n+1)}{2}$.
3. $9,109,209,...$ The $n^{th}$ term in this pattern can also be found by $((n-1) \times 100)+ 9$
   Remember that there are other sequences also to complete the patterns.
   (i) Geometric Sequences- A geometric progression is a sequence of non-zero numbers, where each term after the first is found by multiplying the previous one with a fixed, non-zero number called the common ratio. Example: $1,2,4,8,16,32,64$.
   (ii) Square Numbers- An integer that is the square of an integer is a square number. Example of square number sequence: $1,4,9,16,25,36$.
   (iii) Cube Numbers- A number that is 3 times multiplied by itself is a cube number. Example of cube number sequence: $1,8,27,64,125$. Fibonacci Numbers- Fibonacci numbers are a sequence of numbers such that each number is the sum of the two preceding ones, starting from 0 and 1. Example: $0,1,1,2,3,5,8,13$.