Solveeit Logo
Login

Question

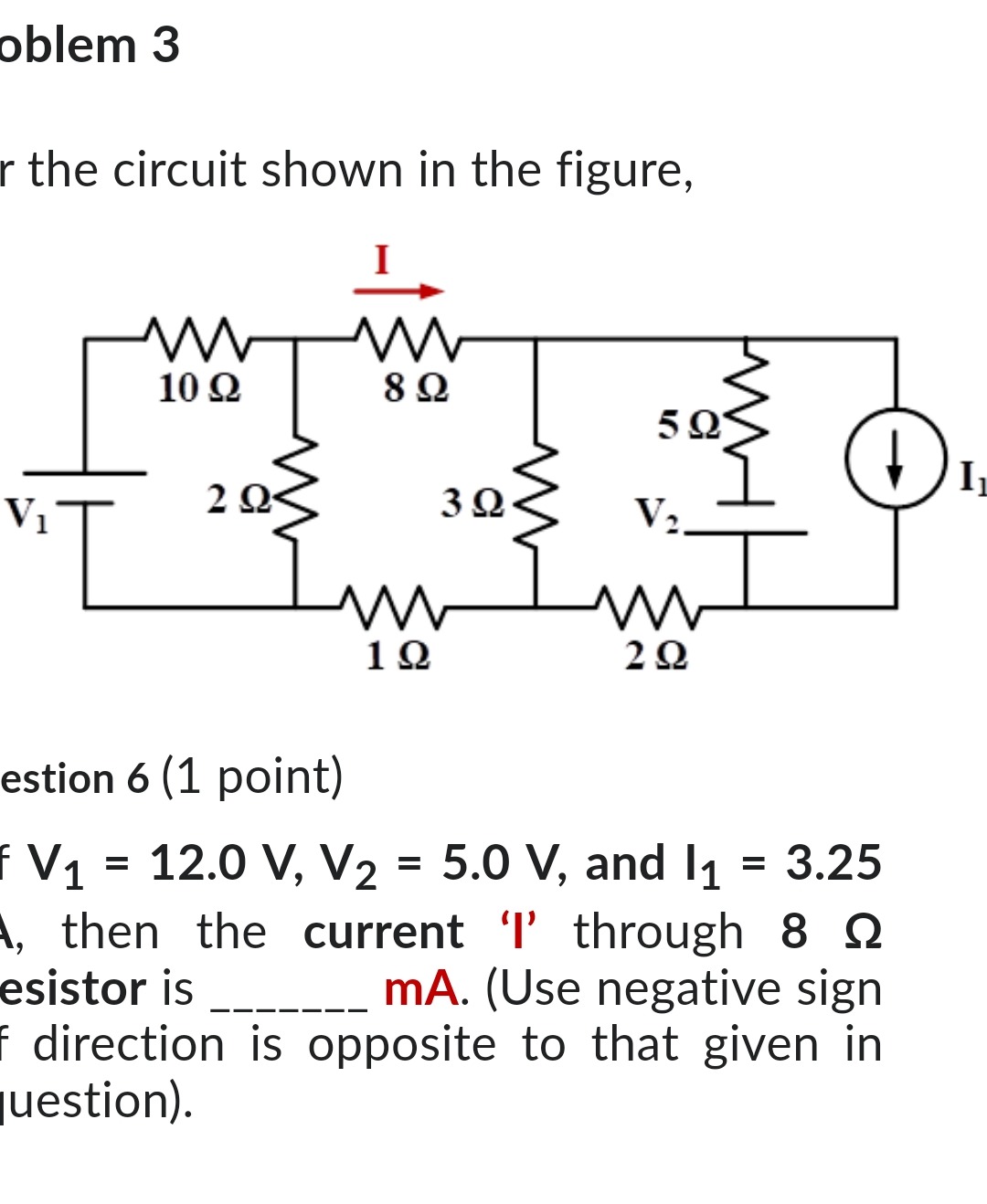
Question: For the circuit shown in the figure, if V₁ = 12.0 V, V₂ = 5.0 V, and I₁ = 3.25 A, then the current '...

For the circuit shown in the figure, if V₁ = 12.0 V, V₂ = 5.0 V, and I₁ = 3.25 A, then the current 'I' through 8 Ω resistor is _______ mA. (Use negative sign if direction is opposite to that given in question).

Answer

1166.67

Explanation

Solution

To find the current 'I' through the 8 Ω resistor, we will use Nodal Analysis.

  1. Define Nodes and Reference:

    • Let the bottom wire be the reference node (ground), with potential 0 V.
    • Let the node connected to the positive terminal of V₁ (and the 10 Ω and 2 Ω resistors) be Node 1. Its potential is V₁ = 12.0 V.
    • Let the node between the 10 Ω, 8 Ω, 2 Ω, and 3 Ω resistors be Node 2. Let its potential be V₂.
    • Let the node between the 8 Ω, 3 Ω, 5 Ω, and V₂ be Node 3. Let its potential be V₃.
    • Let the node between the 2 Ω (bottom right), V₂, and I₁ be Node 4. Let its potential be V₄.

  2. Formulate Node Equations:

    • Relationship between V₃ and V₄: The voltage source V₂ (5.0 V) is connected between Node 3 (positive terminal) and Node 4 (negative terminal). Therefore, V3−V4=V2=5.0 VV_3 - V_4 = V_2 = 5.0 \text{ V}. This implies V4=V3−5.0V_4 = V_3 - 5.0.

    • KCL at Node 4: Currents leaving Node 4:

      1. Through 2 Ω resistor (to ground): I2Ω,bottom=V4−02=V42I_{2\Omega, bottom} = \frac{V_4 - 0}{2} = \frac{V_4}{2}
      2. Through the 5 Ω resistor (from Node 4 to Node 3, but we consider current leaving Node 4): I5Ω=V4−V35I_{5\Omega} = \frac{V_4 - V_3}{5}
      3. Current source I₁ (leaving Node 4 to ground): I1=3.25 AI_1 = 3.25 \text{ A}

      Applying KCL at Node 4: V42+V4−V35+I1=0\frac{V_4}{2} + \frac{V_4 - V_3}{5} + I_1 = 0 Substitute V4=V3−5V_4 = V_3 - 5: V3−52+(V3−5)−V35+3.25=0\frac{V_3 - 5}{2} + \frac{(V_3 - 5) - V_3}{5} + 3.25 = 0 V3−52+−55+3.25=0\frac{V_3 - 5}{2} + \frac{-5}{5} + 3.25 = 0 V3−52−1+3.25=0\frac{V_3 - 5}{2} - 1 + 3.25 = 0 V3−52+2.25=0\frac{V_3 - 5}{2} + 2.25 = 0 V3−52=−2.25\frac{V_3 - 5}{2} = -2.25 V3−5=−4.5V_3 - 5 = -4.5 V3=5−4.5=0.5 VV_3 = 5 - 4.5 = 0.5 \text{ V}

    • KCL at Node 3: Currents leaving Node 3:

      1. Through 8 Ω resistor (to Node 2): I8Ω=V3−V28I_{8\Omega} = \frac{V_3 - V_2}{8}
      2. Through 3 Ω resistor (to ground): I3Ω=V3−03=V33I_{3\Omega} = \frac{V_3 - 0}{3} = \frac{V_3}{3}
      3. Through the 5 Ω resistor (to Node 4): I5Ω=V3−V45I_{5\Omega} = \frac{V_3 - V_4}{5} Since V3−V4=5 VV_3 - V_4 = 5 \text{ V}, this current is 55=1 A\frac{5}{5} = 1 \text{ A}.

      Applying KCL at Node 3: V3−V28+V33+1=0\frac{V_3 - V_2}{8} + \frac{V_3}{3} + 1 = 0 Substitute V3=0.5 VV_3 = 0.5 \text{ V}: 0.5−V28+0.53+1=0\frac{0.5 - V_2}{8} + \frac{0.5}{3} + 1 = 0 0.5−V28+16+1=0\frac{0.5 - V_2}{8} + \frac{1}{6} + 1 = 0 Multiply by LCM(8, 6) = 24: 3(0.5−V2)+4(1)+24(1)=03(0.5 - V_2) + 4(1) + 24(1) = 0 1.5−3V2+4+24=01.5 - 3V_2 + 4 + 24 = 0 29.5−3V2=029.5 - 3V_2 = 0 3V2=29.53V_2 = 29.5 V2=29.53=596 VV_2 = \frac{29.5}{3} = \frac{59}{6} \text{ V}

  3. Calculate Current 'I': The current 'I' is defined as flowing through the 8 Ω resistor from Node 2 to Node 3. I=V2−V38I = \frac{V_2 - V_3}{8} I=596−0.58I = \frac{\frac{59}{6} - 0.5}{8} I=596−368I = \frac{\frac{59}{6} - \frac{3}{6}}{8} I=5668I = \frac{\frac{56}{6}}{8} I=566×8I = \frac{56}{6 \times 8} I=5648I = \frac{56}{48} I=76 AI = \frac{7}{6} \text{ A}

  4. Convert to mA: I=76×1000 mAI = \frac{7}{6} \times 1000 \text{ mA} I=70006 mAI = \frac{7000}{6} \text{ mA} I=35003 mAI = \frac{3500}{3} \text{ mA} I≈1166.67 mAI \approx 1166.67 \text{ mA}

The calculated current I=76 AI = \frac{7}{6} \text{ A} is positive, which means its direction is consistent with the arrow shown in the figure (from left to right).