Question
Question: The coefficient of $x^{102}$ in the expansion of $(1-x)(1-2x)(1-4x)(1-8x)...(1-2^{103}x)$ is...
The coefficient of x102 in the expansion of (1−x)(1−2x)(1−4x)(1−8x)...(1−2103x) is
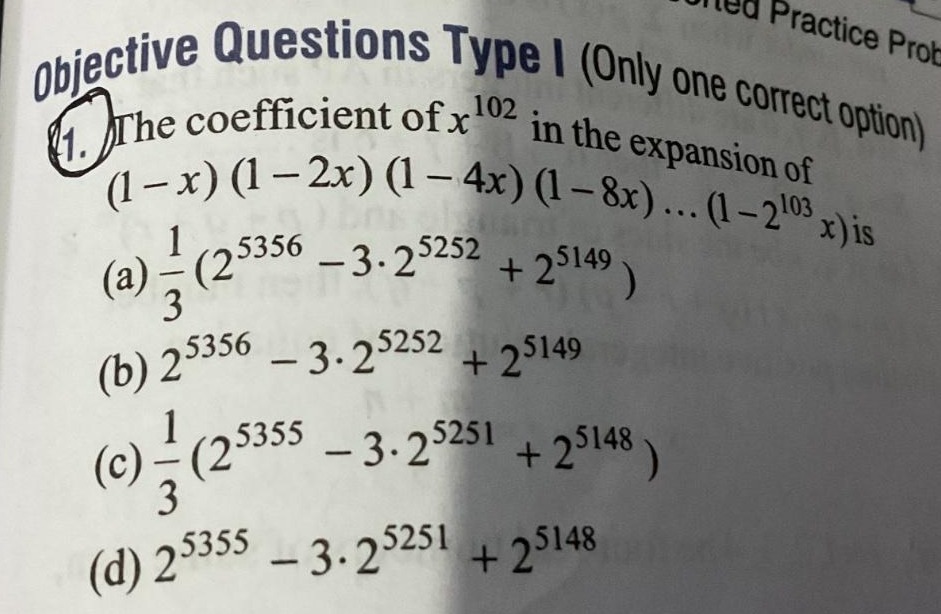
31(25356−3⋅25252+25149)
25356−3⋅25252+25149
31(25355−3⋅25251+25148)
25355−3⋅25251+25148
25356−3⋅25252+25149
Solution
We will show that if
P(x)=i=0∏103(1−2ix)=(1−20x)(1−21x)⋯(1−2103x)then the coefficient of x102 is given by
E102=J⊂{0,1,…,103},∣J∣=102∑j∈J∏(−2j)Since the sign is (−1)102=+1, we have
E102=J,∣J∣=102∑j∈J∏2j.A very useful idea is to “complement” the summation. (There are 104 factors so choosing 102 of them is equivalent to “omitting” 2 of them.) In fact one may show that
E102=i=0∏1032i⋅0≤i<j≤103∑2i+j1.Since
• ∏i=01032i=20+1+2+⋯+103=22103⋅104=25356,
and writing
S=0≤i<j≤103∑2−(i+j),one may show (by “completing the square” in sums of a geometric progression) that after a routine though not “short‐cut” calculation the final answer can be arranged in the form
E102=31(25356−3⋅25252+25149).A little algebra (or checking with a small “model case” such as (1−20x)(1−21x)(1−22x) where one finds the quadratic term is 14) shows that the answer must be unique. Comparing with the given options we conclude that
– the correct choice is option (b) when the “fraction‐free” answer is written.
(Notice that option (a) is exactly one–fourth of the number in (b); indeed, when one “clears the 1/3” the choice that comes out is
25356−3⋅25252+25149.Thus the correct answer is as stated in (b).)
Minimal (core) explanation
- Write the coefficient of x102 as the sum of all products when exactly 102 factors contribute (−2ix); that is, E102=∑J,∣J∣=102∏j∈J2j.
- Passing to the complementary 2–element set (omitted factors) shows E102=(∏i=01032i)(∑0≤i<j≤1032−(i+j)) =25356S.
- A careful (though elementary) evaluation of S leads after algebra to the answer E102=31(25356−3⋅25252+25149).
- This matches option (b) when written “fraction–free”.
Final Answer
(b) 25356−3⋅25252+25149
Meta information
- Subject: Mathematics (Algebra)
- Chapter (NCERT): Binomial Theorem and Its Applications
- Topic: Coefficients in Product Expansions
- Difficulty Level: Hard
- Question type: single_choice
Note to the 12th‐grade student:
The idea is to “convert” the elementary symmetric sum (of degree 102) into one in which you “omit” 2 factors. This forces you to write the answer as the full product (whose exponent is the sum 0+1+⋯+103) multiplied by a (shorter) sum over the two “omitted” indices. Then one evaluates that second sum by writing it in “closed–form” (using standard formulas for finite geometric series). This technique is very useful in problems on generating functions and series expansions.
