Question
Question: O is the centre of an equilateral triangle ABC. \({F_1},{F_2},{F_3}\)are the three forces acting alo...
O is the centre of an equilateral triangle ABC. F1,F2,F3are the three forces acting along the sides AB, BC and AC respectively. What should be the value of F3so that the total torque about O is zero?
A) 2(F1+F2)
B) 2F1+F2
C) F1−F2
D) F1+F2
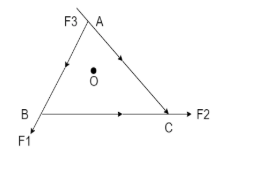
Solution
Recall the concept of torque. When an object rotates around a fixed axis, then the minimum force required to rotate the object is known as torque. It is a vector quantity. Therefore, it has both magnitude and directions. The fixed axis about which the object rotates is known as pivot point.
Step-By-Step solution:
Step I:
Let ‘d’ be the distance of A, B and C from point O. The torque acting on an object can be represented as the product of the force acting and the perpendicular distance from the axis of rotation. Therefore, it is clear from the diagram that the torque acting on B and C is in clockwise direction. But the torque acting on A is in anti clockwise direction.
Step II:
The torque acting on point A is =−F3d
The torque acting on point B is=F1d
And the torque acting on point C is=F2d
Step III:
Equilibrium is a state when all the forces in the system are balanced. A body is said to be in rotational equilibrium if the sum of torques acting on the system about an axis is equal to zero. Therefore according to this condition,
F1d+F2d−F3d=0
d(F1+F2−F3)=0
F1+F2−F3=0
F3=F1+F2
Step IV:
Hence when F3=F1+F2then the torque acting on the system will be equal to zero.
⇒ Option D is the right answer.
Note: It is to be noted that sometimes torque is confused with work. Where torque is a vector quantity, work is a scalar quantity. The component of distance in torque is perpendicular to the axis, whereas the component of distance in work is parallel to the body.
