Question

O is the centre of a circle. Its diameter is $80cm$. $P$ is at $58cm$from $O$. Two tangents to the circle drawn from $P$ touch to the circle at points $Q$ and $R$. Find the perimeter of $\square PQOR$.

Answer 1

Hint : In order to find the perimeter of $\square PQOR$, we will be finding the lengths of $OQ$ and $OR$firstly. Since we are given that the distance from the centre to the point $P$ is $58cm$, that would also be considered. Then we will be finding the length of $PQ$ and $PR$ by applying the Pythagoras theorem. After obtaining all the required lengths, we will be adding up all the lengths to obtain the perimeter of $\square PQOR$.

Complete step-by-step solution:
Now let us learn about circles and tangents. A line that touches the circle at a point is called the tangent of the circle. The point at which the circle and tangent meet is called the point of tangency. We can find the equation of tangent of circle having the equation of circle as ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ by $x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}$.
Now let us find the perimeter of $\square PQOR$.

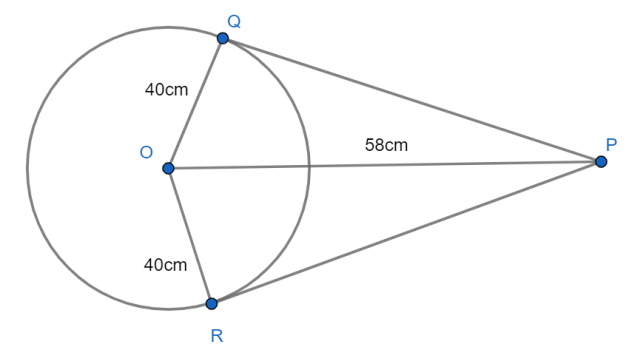
We know that the lengths of $OQ$ and $OR$ are $40cm$because they are the radii of the circle and we are told that the diameter measures $80cm$. So the half of $80cm$ would be the measure of the $OQ$ and $OR$ i.e. $40cm$.
We can observe that the $\Delta POQ$ and $\Delta POR$ form the right angled triangles.
So we can find the lengths of $PQ$ and $PR$by applying the Pythagoras theorem.
So let us consider the triangle $\Delta POQ$.
We know that, $P{{Q}^{2}}+O{{Q}^{2}}=P{{O}^{2}}$

& P{{Q}^{2}}+O{{Q}^{2}}=P{{O}^{2}} \\\ & \Rightarrow P{{Q}^{2}}+{{40}^{2}}={{58}^{2}} \\\ & \Rightarrow P{{Q}^{2}}={{58}^{2}}-{{40}^{2}} \\\ & \Rightarrow P{{Q}^{2}}=3364-1600 \\\ & \Rightarrow PQ=\sqrt{1764}=42 \\\ \end{aligned}$$ The length of $$PQ$$ and $$PR$$ are equal as they originate from the same point and end at the same circle. $$\therefore PR=42cm$$ Now we have obtained all the required lengths of $$\square PQOR$$. Now we will be summing up the values, we get $$\Rightarrow 40cm+40cm+42cm+42cm=164cm$$ $$\therefore $$ The perimeter of $$\square PQOR$$ is $$164cm$$. **Note:** While solving such problems, we must have a note regarding the formation of the right angle correctly. Wrongly choosing the angle can provide us with incorrect length of sides. Also, we must know that the lengths of tangents of a circle from the same point are equal because solving it to find the length of both the tangents is time consuming.