Question

Number of ways in which a person can walk up a stairway which has 7 steps if he can take 1 or 2 steps up the stair at a time, is
A.28
B.21
C.15
D.17

Answer 1

Here, we have to use the concept of combination to find the number of ways in which a person can walk up a stairway which has 7 steps. Combination is used when we have to choose various ways in which objects from a set may be selected. So, we have to make pairs of the combination of 1 and 2 steps and then by using the concept of the combination we will get the number of ways a person can walk up a stairway.

Complete step-by-step answer:
It is given that there are 7 steps of the stairway and he can take only 1 or 2 steps up the stairs at a time.
Now we have to make the pair of steps taken by the person like how many 1 steps and 2 steps taken by the person. Therefore we get
So to walk up the stairway a person can take seven 1 steps and zero 2 steps or he can take five 1 steps and one 2 step or he can take three 1 steps and two 2 steps or he can take one 1 step and three 2 steps
So we can write this pairs of 1 step and 2 step in the form of a table and its number of ways in the table, we get

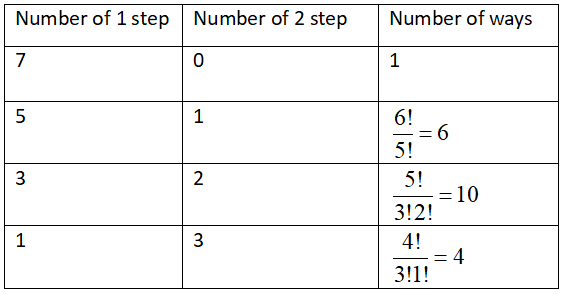
So by adding all the ways we will get the total number of ways a person can walk up a stairway.
Therefore, total number of ways $= 1 + 6 + 10 + 4 = 21$
Hence, a person can walk up a stairway which has 7 steps if he can take 1 or 2 steps up the stair at a time in 21 different ways.
So, option B is the correct option.

Note: Permutations may be defined as the different ways in which a collection of items can be arranged. For example: The different ways in which the numbers 1, 2 and 3 can be grouped together, taken all at a time, are$123,{\rm{ }}132,{\rm{ }}213,{\rm{ }}231,{\rm{ }}312,{\rm{ }}321$.
So, Number of permutations of n things, taken r at a time, denoted by ${}^{\rm{n}}{{\rm{P}}_{\rm{r}}} = \dfrac{{{\rm{n}}!}}{{{\rm{(n - r)}}!}}$
Combinations may be defined as the various ways in which objects from a set may be selected. For example: The different selections possible from the numbers 1, 2, 3 taking 2 at a time, are ${\rm{12, 23 \, and\, 31}}$
So, Number of combinations possible from n group of items, taken r at a time, denoted by $^{\rm{n}}{{\rm{C}}_{\rm{r}}} = \dfrac{{{\rm{n}}!}}{{{\rm{r}}!{\rm{(n - r)}}!}}$