Question
Question: Number of solutions of the equation \[{x^3} - \left[ x \right] = 3\] is (where \[\left[ . \right]\] ...
Number of solutions of the equation x3−[x]=3 is (where [.] represents the greatest integer function)
a.0
b.1
c.2
d.3
Solution
Here, we will plot the coordinates and then check for the equality of the given equations. The function which is rounding off the real number down to the integer less than the number is known as the greatest integer function.
Complete step-by-step answer:
We are given that x3−[x]=3
Now, we are rewriting the equation as
⇒x3=[x]+3…………………………….(1)
Now, substituting x=0 in the equation (1), we get
03=0+3 ⇒0=3
Now, substituting x=1in the equation (1), we get
13=1+3 ⇒1=4
Now, substituting x=2in the equation (1), we get
23=2+3
⇒8=5
Since it does not solve the equation correctly, we are assuming that the plot for the co-ordinates of the solved equation is not satisfying the relation.
Now, plotting the co-ordinates, we get
Since we are assuming that y=x3 , so we get
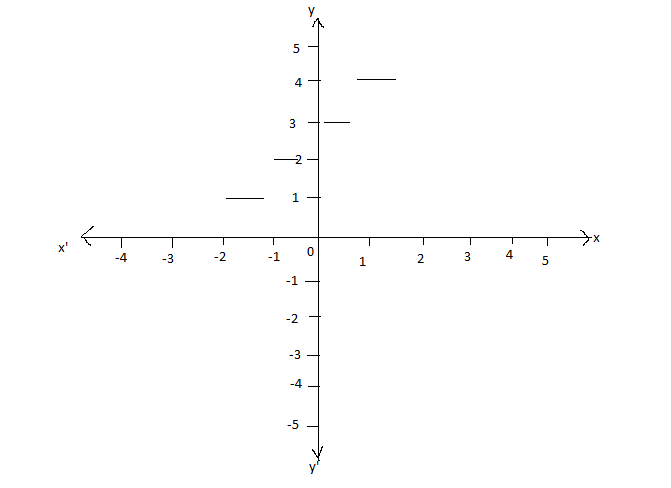
At x=(4)31 , we have x≅1.587
Thus, [x]=1
x3=4
⇒x3=1+3
⇒x3−3=1
Thus, we have only one solution.
Therefore, the Number of solutions of the equation x3−[x]=3 is 1. Thus Option(B) is the correct answer.
Note: We can also plot the graph and draw the curves to find the number of solutions of the equation.
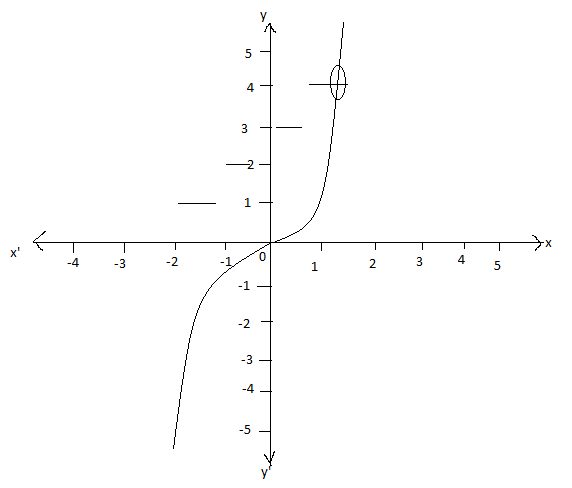
The curve intersecting the point is at only one point. So, the number of solutions of the equation x3−[x]=3 is 1.
We should also know that the number of intersection points of the curves and the co-ordinates determines the number of solutions of the equation. The greatest functions are always piecewise continuous. The graph of greatest functions is viewed as steps and thus it is called as step function or floor function.
