Question

Number of solutions of the equation $3x + \{x\} = 4[x]$ will be (where [ ] & { } represent greatest integer and fractional part respectively)

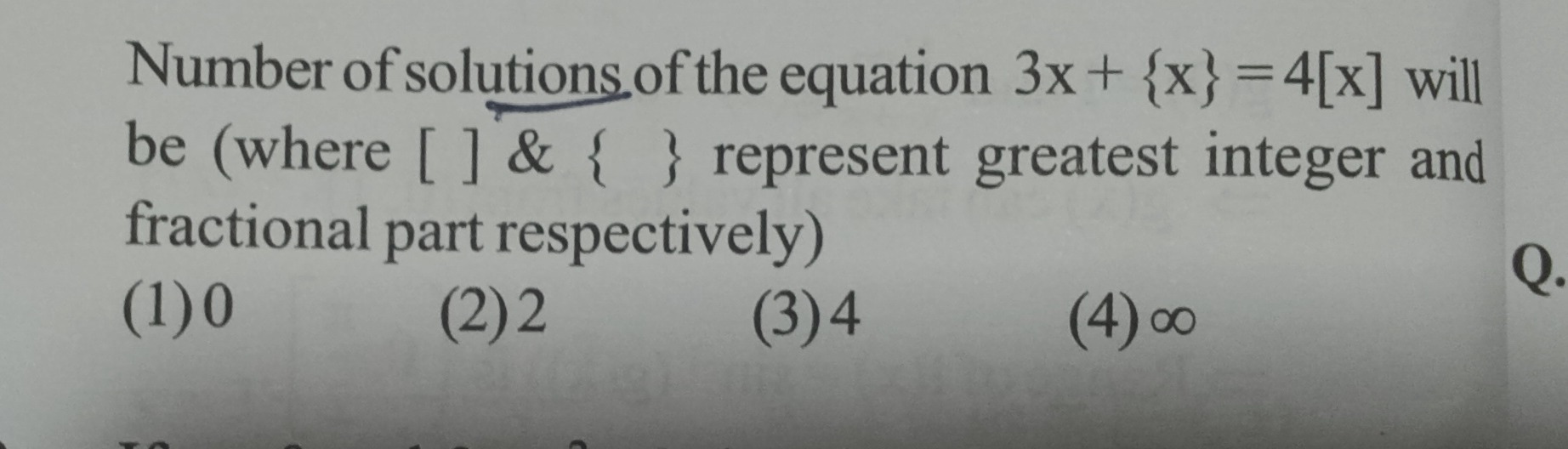
• A. 0
• B. 2
• C. 4
• D. $\infty$

Answer 1

Answer: (C)

The number of solutions is 4.

Answer 2

The given equation is $3x + \{x\} = 4[x]$. We know that any real number $x$ can be written as $x = [x] + \{x\}$, where $[x]$ is the greatest integer less than or equal to $x$, and $\{x\}$ is the fractional part of $x$, such that $[x]$ is an integer and $0 \le \{x\} < 1$.

Substitute $x = [x] + \{x\}$ into the equation:

$3([x] + \{x\}) + \{x\} = 4[x]$

$3[x] + 3\{x\} + \{x\} = 4[x]$

$3[x] + 4\{x\} = 4[x]$

Rearrange the terms to isolate $\{x\}$:

$4\{x\} = 4[x] - 3[x]$

$4\{x\} = [x]$

Let $[x] = n$ and $\{x\} = f$. The equation becomes $4f = n$. We know that $f = \{x\}$ must satisfy the condition $0 \le f < 1$. Substitute $f = n/4$ into this inequality:

$0 \le \frac{n}{4} < 1$

Multiply the inequality by 4:

$0 \le n < 4$

Since $n = [x]$ must be an integer, the possible integer values for $n$ are $0, 1, 2, 3$.

For each possible integer value of $n = [x]$, we find the corresponding value of $\{x\} = n/4$:

1. If $[x] = 0$, then $\{x\} = 0/4 = 0$. This is valid since $0 \le 0 < 1$. The solution is $x = [x] + \{x\} = 0 + 0 = 0$.

2. If $[x] = 1$, then $\{x\} = 1/4$. This is valid since $0 \le 1/4 < 1$. The solution is $x = [x] + \{x\} = 1 + 1/4 = 5/4$.

3. If $[x] = 2$, then $\{x\} = 2/4 = 1/2$. This is valid since $0 \le 1/2 < 1$. The solution is $x = [x] + \{x\} = 2 + 1/2 = 5/2$.

4. If $[x] = 3$, then $\{x\} = 3/4$. This is valid since $0 \le 3/4 < 1$. The solution is $x = [x] + \{x\} = 3 + 3/4 = 15/4$.

Any other integer value for $[x]$ would result in $\{x\} = [x]/4$ being outside the range $[0, 1)$. For example, if $[x]=4$, $\{x\}=1$, which is not allowed. If $[x]=-1$, $\{x\}=-1/4$, which is not allowed.

Thus, there are exactly four possible integer values for $[x]$ that yield a valid fractional part $\{x\}$. Each of these pairs corresponds to a unique solution for $x$. The solutions are $x=0, 5/4, 5/2, 15/4$. The number of solutions is 4.