Question
Question: Number of integers satisfying the inequality $log_2 \sqrt{x} - 2log_{1/4}^2 x + 1 > 0$ is...
Number of integers satisfying the inequality log2x−2log1/42x+1>0 is
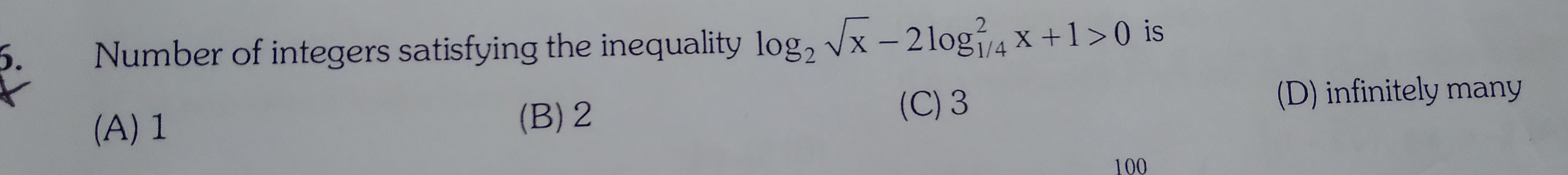
1
2
3
infinitely many
3
Solution
The given inequality is log2x−2log1/42x+1>0. The domain requires x>0.
We simplify the logarithmic terms:
- log2x=log2x1/2=21log2x.
- For log1/4x, we use the change of base formula logba=logcblogca: log1/4x=log2(1/4)log2x=log2(2−2)log2x=−2log2x=−21log2x. Therefore, log1/42x=(−21log2x)2=41(log2x)2.
Substitute these into the inequality: 21log2x−2(41(log2x)2)+1>0 21log2x−21(log2x)2+1>0
Let y=log2x. The inequality becomes: 21y−21y2+1>0
Multiply the inequality by 2 to clear the fractions: y−y2+2>0
Rearrange into a standard quadratic form and multiply by -1 (reversing the inequality sign): y2−y−2<0
Factor the quadratic expression: (y−2)(y+1)<0
This inequality holds for values of y between the roots -1 and 2: −1<y<2
Substitute back y=log2x: −1<log2x<2
Since the base of the logarithm is 2>1, the exponential function 2t is increasing. Exponentiating with base 2 preserves the inequality direction: 2−1<x<22 21<x<4
We need to find the number of integers satisfying this inequality. The integers in the interval (21,4) are 1,2, and 3. There are 3 such integers.
