Question

Number of elements in exactly one of the sets $A$ ,$B$ ,$C$
$= n\left( A \right) + n\left( B \right) + n\left( C \right) - 2n\left( {A \cap B} \right) - 2n\left( {B \cap C} \right) - 2n\left( {A \cap C} \right) + 3n\left( {A \cap B \cap C} \right)$

Answer 1

To solve this type of problem always draw the Venn diagram to simplify the question. From the Venn diagram we will write the statements for each of the sets $A$ ,$B$ and $C$. To find the number of elements which are exactly in one of them we will have to find the shaded region as shown in the Venn diagram. The shaded region is the reason which we will get by subtracting the number of elements which are the intersection of the other two from the number of elements in the set itself.

Complete step-by-step solution:
The following is the Venn diagram,

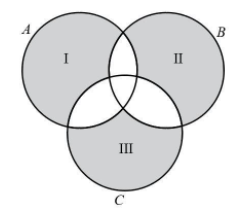
From the Venn diagram We will find the shaded region $I$ , $II$ and $III$ respectively.

The number of elements in exactly set $A$ is the shaded region $I$ and that can be expressed as,
$I = n\left( A \right) - n\left( {A \cap B} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)$

Here, $\left( {A \cap B} \right)$ indicates the intersection between two sets A and B which means that all the elements of set A belongs to set B. Similarly, $\left( {A \cap C} \right)$ indicates the intersection between two sets A and C which means that all the elements of set A belong to set C and $\left( {A \cap B \cap C} \right)$ indicates that all the elements of set A belongs to B as well as all the elements of set B belong to C.

The number of elements in exactly set $B$ is the shaded region $II$ and that can be expressed as,
$II = n\left( B \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right)$

Here, $\left( {B \cap C} \right)$ indicates the intersection between two sets B and C which means that all the elements of set B belong to set C.

The number of elements in exactly set $C$ is the shaded region $III$ and that can be expressed as,
$III = n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right)$

Now on adding the above three region we will get the number of elements in exactly one of the sets $A$ ,$B$ ,$C$ is,
$I + II + III = n\left( A \right) - n\left( {A \cap B} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right) + n\left( B \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) + n\left( {A \cap B \cap C} \right)\\\ = n\left( A \right) + n\left( B \right) + n\left( C \right) - 2n\left( {A \cap B} \right) - 2n\left( {A \cap C} \right) - 2n\left( {B \cap C} \right) + 3n\left( {A \cap B \cap C} \right)$

Hence it is proved that The number of elements in exactly one of the sets $A$ ,$B$ ,$C$ is,
$= n\left( A \right) + n\left( B \right) + n\left( C \right) - 2n\left( {A \cap B} \right) - 2n\left( {B \cap C} \right) - 2n\left( {A \cap C} \right) + 3n\left( {A \cap B \cap C} \right)$

Note: The union of sets can be defined as the number of elements which are present in at least one of the sets and the intersection of sets can be defined as the number of elements that are present in all the sets. $\cup$ represents union of sets and $\cap$ represents intersection of the sets. For the number of elements exactly in a set, subtract the number of elements which are common in all the sets from the number of elements in the set itself.