Question
Question: Number of different paths of the shortest distance from A to B in the grid which do not pass through...
Number of different paths of the shortest distance from A to B in the grid which do not pass through M is,
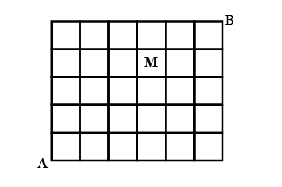
Solution
To find the total probability required to cross the path or grid from A to B is by counting the total number of grids both horizontal and vertical and by removing a single line of block from both the vertical and horizontal, column and rows respectively by using the formula as:
Total rows and columnCNumber of ways passing through M.
Complete step by step solution:
The total number of short distance path that can be used when crossing through M is given down below:
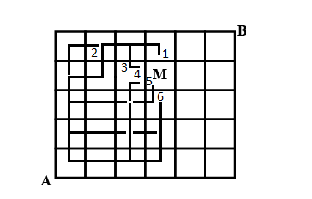
Now as we can see in the above diagram the number of ways the line passes through M to get to B is by six different ways.
To find the total number of ways in which the path from A to B can be taken is first we need to establish the total number of paths without avoiding M.
So let us see that the width and the length of the grid is given as \6\times 6\hence, the total number of paths from A to B is 6+6=12and now the total number of ways while avoiding M is 12-1=11as whenever we will move we will avoid at least one cell at a time either a column cell or a row cell thereby making the total number of paths 11.
Therefore, the total number of paths one can take to go from A to B while avoiding M is by using the combination formula of Total rows and columnCNumber of ways passing through M:
⇒11C6=6!5!11!
After deducting the factorial value of 5 on both numerator and denominator:
