Question
Question: Now consider the partition to be free to move without friction so that the pressure of gases in both...
Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. Then total work done by the gases till the time they achieve equilibrium will be
A. 250R
B. 200R
C. 100R
D. −100R
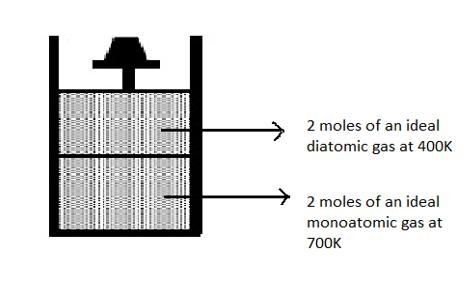
Solution
The concept to be used is of heat transfer in an adiabatic process in which the process takes place at constant temperature.
The concept of heat capacity at constant pressure is to be used which is different for ideal monoatomic as well ideal diatomic gas.
Also, one should know the formula for work done which will take place as the volume and temperature of both compartments change to attain a condition of equilibrium.
Complete answer:
The whole process takes place maintaining constant pressure
So according to the points mentioned in the hint, we will find the final temperature of the system.
Heat evolved or gained at constant temperature is given by n×Cp×ΔT
, Cpis the heat capacity at constant pressure.
Heat capacity for monoatomic gas=25R
Heat capacity for diatomic gas=27R
Let the final temperature be T
Heat lost by lower compartment =2×25R×(700−T)
Heat gained by lower compartment =2×27R×(T−400)
As we know it is an isolated system so heat released by the lower compartment at constant pressure is gained by the lower compartment.
Equating above equations,
2×25R×(700−T)=2×27R×(T−400)
⇒12T=6300
T=525K
Also work done =nR(TFinal−TInitial)
Work done by lower gas:
⇒2×R×(525−700)
⇒−350RJoules
Work done by upper gas:
⇒2×R×(525−400)
⇒250RJoules
Net work done=−350R+250R=−100RJoules
Hence the correct option is D.
Note:
During a process involving constant temperature, the internal energy of the gas remains constant as it is a function of temperature.
The heat capacity at constant pressure or at constant volume is dependent on the degree of freedom of a gas.
