Question

If 2 tan⁻¹(cos x) = tan⁻¹(2 cosec x) then sinx + cosx =

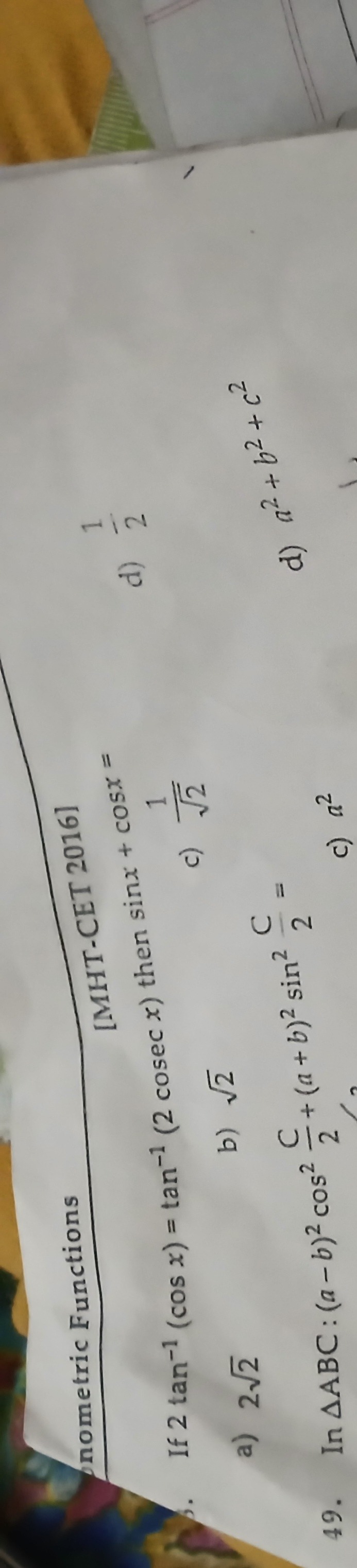
• A. 2√2
• B. √2
• C. $\frac{1}{\sqrt{2}}$
• D. $\frac{1}{2}$

Answer 1

Answer: (B)

√2

Answer 2

To solve the equation $2 \tan^{-1}(\cos x) = \tan^{-1}(2 \csc x)$, we take the tangent of both sides. Using the identity $\tan(2A) = \frac{2 \tan A}{1 - \tan^2 A}$ with $A = \tan^{-1}(\cos x)$, we have:

$$\tan(2 \tan^{-1}(\cos x)) = \frac{2 \cos x}{1 - \cos^2 x} = \frac{2 \cos x}{\sin^2 x}$$

Also, $\tan(\tan^{-1}(2 \csc x)) = 2 \csc x = \frac{2}{\sin x}$. Equating the two expressions:

$$\frac{2 \cos x}{\sin^2 x} = \frac{2}{\sin x}$$ $$\cos x = \sin x$$ $$\tan x = 1$$ $$x = \frac{\pi}{4} + k\pi, \quad k \in \mathbb{Z}$$

For the principal value $x = \frac{\pi}{4}$, we have:

$$\sin x + \cos x = \sin \frac{\pi}{4} + \cos \frac{\pi}{4} = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} = \frac{2}{\sqrt{2}} = \sqrt{2}$$

Therefore, $\sin x + \cos x = \sqrt{2}$.