Question

no. of fn. $f:A \rightarrow B$ with $f(a) \neq 1$ or $f(b) \neq 2$ or both

A: {a,b,c,d}

B: {1,2,3,4,5,6}

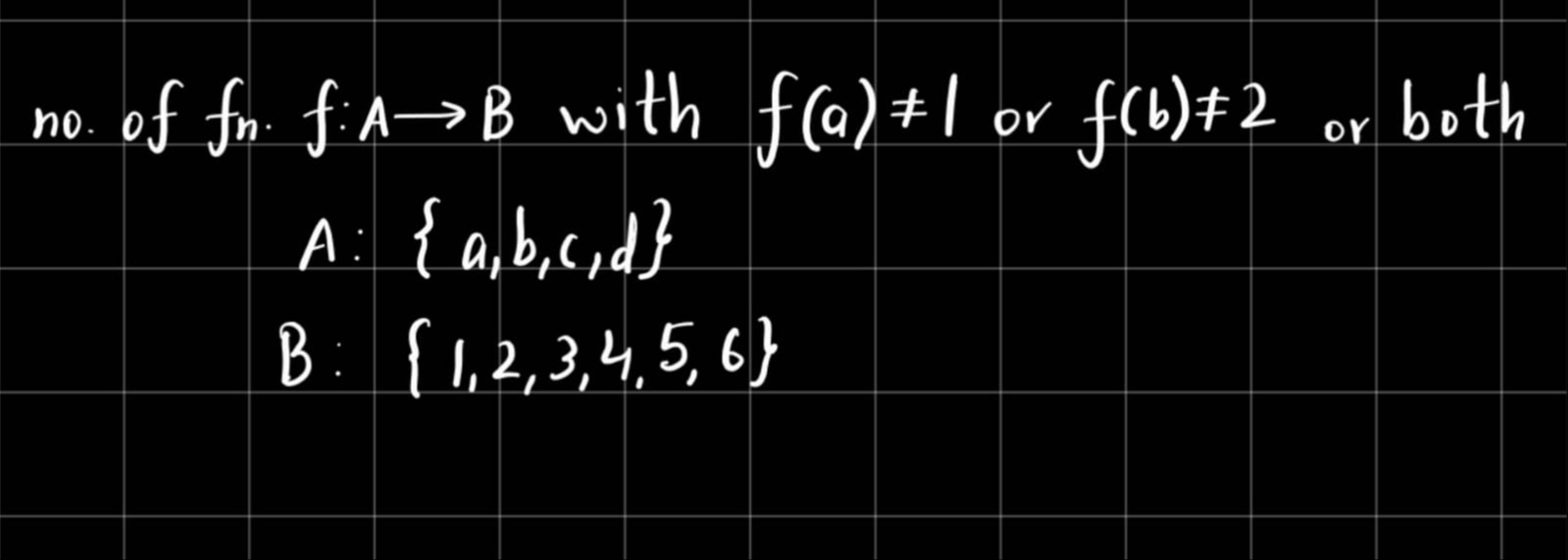
Answer 1

1260

Answer 2

The total number of functions from $A$ to $B$ is:

$$6^4 = 1296.$$

We need functions with $f(a) \neq 1$ or $f(b) \neq 2$ (or both). This set is the complement of the functions satisfying

$$f(a) = 1 \quad \text{and} \quad f(b) = 2.$$

The number of functions with $f(a)=1$ and $f(b)=2$ is:

$$6^2 = 36.$$

Thus, the required number is:

$$1296 - 36 = 1260.$$