Question
Question: Nine identical discs, each of mass m and radius R, are arranged in the same plane as shown in figure...
Nine identical discs, each of mass m and radius R, are arranged in the same plane as shown in figure. Find moment of inertia of the system about the axis AA’ which passes through the center of the central disc as indicated by line in the figure. This axis AA makes 45∘ with x-axis.
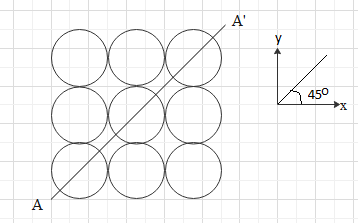
Explanation
Solution
Here we have to find the moment of inertia I of the system about the axis AA’, which will be given as the sum of moment of inertia at the ends of the axis. So first we will redraw the given diagram to specify the points at which we will be finding I. Also it is given that the axis makes 45∘ along with x axis and we can see from the given diagram it also makes 45∘ with y-axis.
Formula used:
& I={{I}_{x}}+{{I}_{y}}+{{I}_{z}} \\\ & I=\dfrac{M{{R}^{2}}}{4}\left( 1+{{\sin }^{2}}\theta \right) \\\ \end{aligned}$$ **Complete answer:** Let us first redraw the diagram, and label it so as to find the moment of inertia of the system about the axis AA’. 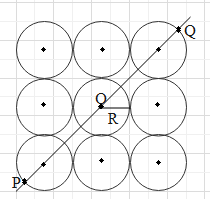 Now the moment of inertia along the axis would be given as the sum of moment of inertia at point P and Q. From the above diagram and given data, distance of OP and OQ is the same as the disc are identical having the same radius, also the mass of each disc is the same. Therefore, the moment of inertia at point P will be the same as Q. So the moment of inertia along the axis can be given as twice the moment of inertia at point P. First of all, let us find the moment of inertia for single disc which will be given here by $$I={{I}_{x}}+{{I}_{y}}+{{I}_{z}}$$ Where $${{I}_{x}},{{I}_{y}}\text{ and }{{I}_{z}}$$can be given as $$I=\dfrac{M{{R}^{2}}}{4}\left( 1+{{\sin }^{2}}\theta \right)$$ Where θ is the angle made by the axis of the plane along with the x-axis or y-axis or z-axis. Here we have given that the given axis makes $$45{}^\circ $$with x-axis and mass is m and radius of disc is R, then moment of inertia along x-axis will be given as $$\begin{aligned} & {{I}_{x}}=\dfrac{m{{R}^{2}}}{4}\left( 1+{{\sin }^{2}}45{}^\circ \right) \\\ & \Rightarrow {{I}_{x}}=\dfrac{m{{R}^{2}}}{4}\left( 1+{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}} \right) \\\ & \Rightarrow {{I}_{x}}=\dfrac{m{{R}^{2}}}{4}\left( 1+\dfrac{1}{2} \right) \\\ & \Rightarrow {{I}_{x}}=\dfrac{m{{R}^{2}}}{4}\left( \dfrac{3}{2} \right) \\\ & \Rightarrow {{I}_{x}}=\dfrac{3m{{R}^{2}}}{8} \\\ \end{aligned}$$ From the diagram given in the question the axis also makes $$45{}^\circ $$ with the y-axis. So the moment of inertia along y-axis will be equal to x-axis $${{I}_{y}}=\dfrac{3m{{R}^{2}}}{8}$$ Now given axis will make $$90{}^\circ $$with z-axis, so the moment of inertia along z-axis will be $$\begin{aligned} & {{I}_{z}}=\dfrac{m{{R}^{2}}}{4}\left( 1+{{\sin }^{2}}90{}^\circ \right) \\\ & \Rightarrow {{I}_{z}}=\dfrac{m{{R}^{2}}}{4}\left( 1+{{\left( 1 \right)}^{2}} \right) \\\ & \Rightarrow {{I}_{z}}=\dfrac{m{{R}^{2}}}{4}\left( 1+1 \right) \\\ & \Rightarrow {{I}_{z}}=\dfrac{m{{R}^{2}}}{4}\left( 2 \right) \\\ & \Rightarrow {{I}_{z}}=\dfrac{m{{R}^{2}}}{2} \\\ \end{aligned}$$ Now total I will be $$\begin{aligned} & I=\dfrac{3m{{R}^{2}}}{4}+\dfrac{3m{{R}^{2}}}{4}+\dfrac{m{{R}^{2}}}{2} \\\ & \Rightarrow I=\dfrac{m{{R}^{2}}(3+3+2)}{4} \\\ & \Rightarrow I=\dfrac{8m{{R}^{2}}}{4} \\\ & \Rightarrow I=2m{{R}^{2}} \\\ \end{aligned}$$ Now moment of inertia at point P will be given as $$\begin{aligned} & {{I}_{P}}={{I}_{O}}+9I \\\ & \Rightarrow {{I}_{P}}={{I}_{O}}+9(2m{{R}^{2}}) \\\ & \Rightarrow {{I}_{p}}={{I}_{O}}+18m{{R}^{2}}\text{ }...............\text{(i)} \\\ \end{aligned}$$ Here $${{I}_{O}}$$is the moment of inertia at point O as it is the center of the axis and the second term, I is the moment of inertia we calculated. It is multiplied with 9 as there are a total of nine discs. Now $${{I}_{O}}$$is given as a sum of moment of inertia along the center of mass and the moment of inertia due to the disc attached to it. From the given diagram 4 discs are connected directly to the central disc and four are indirectly which are in the corners. The radius for the discs connected directly will be 2R i.e. the distance of center of the central axis from the center on disc connected directly to it and for the corner discs it will be 3R i.e. distance of center of corner disc from the center of central disc. $$\begin{aligned} & {{I}_{O}}={{I}_{CM}}+4\left[ 2m{{\left( 3R \right)}^{2}} \right]+4\left[ 2m{{(2R)}^{2}} \right] \\\ & \Rightarrow {{I}_{O}}=\dfrac{m{{R}^{2}}}{2}+4\left[ 2m(9{{R}^{2}}) \right]+4\left[ 2m(4{{R}^{2}}) \right] \\\ & \Rightarrow {{I}_{O}}=\dfrac{m{{R}^{2}}}{2}+4(18m{{R}^{2}})+4(8m{{R}^{2}}) \\\ & \Rightarrow {{I}_{O}}=\dfrac{m{{R}^{2}}}{2}+72m{{R}^{2}}+32m{{R}^{2}} \\\ & \Rightarrow {{I}_{O}}=\dfrac{209m{{R}^{2}}}{2} \\\ \end{aligned}$$ Substituting this value in equation (i), we get $$\begin{aligned} & {{I}_{p}}=\dfrac{209m{{R}^{2}}}{2}+18m{{R}^{2}} \\\ & \Rightarrow {{I}_{P}}=\dfrac{245m{{R}^{2}}}{2} \\\ \end{aligned}$$ Now as discussed earlier the moment of inertia along the axis AA’ will be twice of moment of inertia at point P, therefore $$\begin{aligned} & {{I}_{AA'}}=2{{I}_{P}} \\\ & \Rightarrow {{I}_{AA'}}=2\times \dfrac{245m{{R}^{2}}}{2} \\\ & \Rightarrow {{I}_{AA'}}=245m{{R}^{2}} \\\ \end{aligned}$$ Here $${{I}_{AA'}}$$ is the moment of inertia along the given axis. Hence we got the value for the moment of inertia along the axis AA’. **Note:** The moment of inertia with respect to the center of mass is calculated along the z-axis, therefore its value is given by the value of moment of inertia along the z-axis. Also here we assume the distance of the gap is R. Here we used the parallel axis theorem to calculate the moment of inertia at point P and at point O.