Question

Net positive charge on the inner spherical conductor is $3Q$ and on the outer spherical conductor is $Q$. Switch is closed.

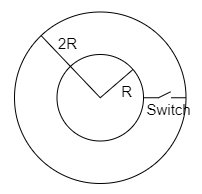
(A) charge will flow from inner shell to outer shell
(B) charge will flow from outer shell to inner shell
(C) charge will not flow
(D) none of these

Answer 1

Already we know that the charge will flow from high charge to the low charge. By determining the total charge of the system, and then equating the potential due to two shells are the same. Then the charge relation can be determined. And by using the total charge equation, the individual charge can be determined.

Useful formula
The electric potential is given by,
$V = \dfrac{Q}{R}$.
Where, $V$ is the electric potential, $Q$ is the charge and $R$ is the distance.

Complete step by step solution
Given that,
The charge of the outer shell is, $Q$,
The charge of the inner shell is $3Q$.
The total charge of the system is equal to the sum of the individual charges, $\Rightarrow Q + 3Q = 4Q$.
The initial energy before the switch is closed on $2R$ is $Q$,
The initial energy before the switch is closed on $R$ is $3Q$.
After the switch is closed, then
Now by equating the electric potential of the two shells are same, then
${V_1} = {V_2}$
Where, ${V_1}$ is the electric potential of the outer shell and ${V_2}$ is the electric potential of the inner shell.
Then the above equation is written as,
$\dfrac{{{Q_1}}}{{2R}} = \dfrac{{{Q_2}}}{R}$
Where, ${Q_1}$ is the charge of the outer shell after the switch is closed and ${Q_2}$ is the charge of the inner shell after the switch is closed.
By cancelling the terms in the above equation, then
$\dfrac{{{Q_1}}}{2} = \dfrac{{{Q_2}}}{1}$
By rearranging the terms, then
${Q_1} = 2{Q_2}$
The total charge of the system is,
${Q_1} + {Q_2} = 4Q$
By substituting the value of the ${Q_1}$ in the above equation, then
$2{Q_2} + {Q_2} = 4Q$
By adding the terms, then
$3{Q_2} = 4Q$
By rearranging the terms, then
${Q_2} = \dfrac{4}{3}Q$
On dividing the terms, then
${Q_2} = 1.33Q$
Substituting the ${Q_2}$ value in the equation of ${Q_1}$, then
${Q_1} = 2 \times 1.33Q$
On multiplying the terms, then
${Q_1} = 2.66Q$
By comparing the values of ${Q_1}$ and ${Q_2}$, the charge in ${Q_1}$ is higher.
So, the charge flows from the outer shell to the inner shell.

Hence, the option (B) is the correct answer.

Note: The charge flows from high charge to the low charge, so that the outer shell has the higher charge than the inner shell after the switch between the outer shell and the inner shell is closed. By adding the charge of the outer shell and the inner shell is equal to the total charge of the system.