Question

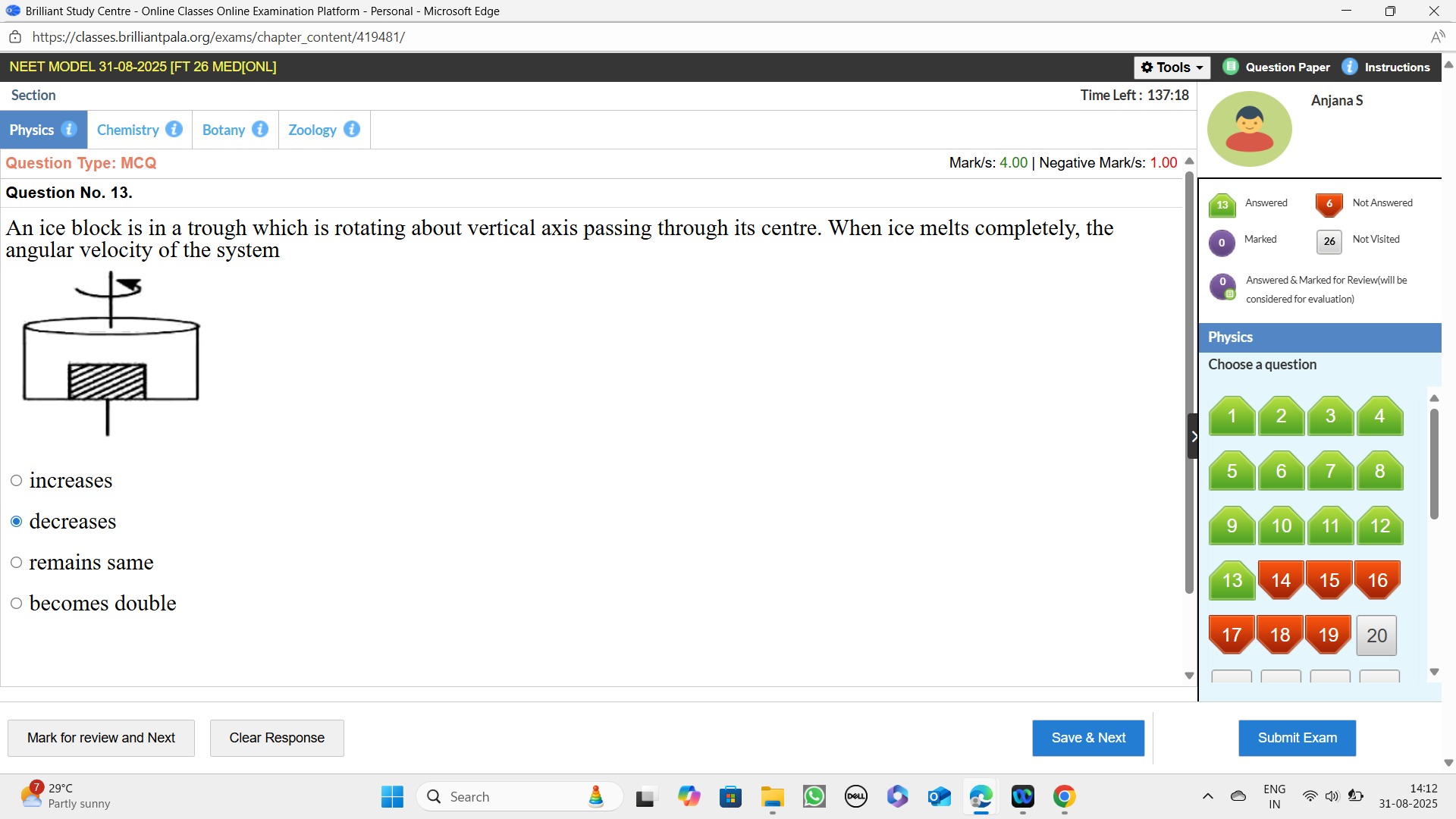
An ice block is in a trough which is rotating about vertical axis passing through its centre. When ice melts completely, the angular velocity of the system

• A. increases
• B. decreases
• C. remains same
• D. becomes double

Answer 1

Answer: (B)

decreases

Answer 2

The system consists of a trough and an ice block rotating about a vertical axis. The angular momentum of the system is conserved as there are no external torques acting on it. The angular momentum ($L$) is given by the product of the moment of inertia ($I$) and the angular velocity ($\omega$): $L = I\omega$.

When the ice melts, it turns into water. Water is a liquid, and in a rotating system, liquids tend to spread out radially due to centrifugal forces. This means that the mass distribution shifts to larger radial distances from the axis of rotation.

The moment of inertia ($I$) of a system is calculated as $I = \int r^2 dm$, where $r$ is the distance from the axis of rotation and $dm$ is an infinitesimal mass element. If the mass distribution shifts to larger radii, the moment of inertia of the system increases.

Since the angular momentum ($L$) is conserved ($L_i = L_f$), we have $I_i \omega_i = I_f \omega_f$. As the moment of inertia increases ($I_f > I_i$) due to the spreading of water, the angular velocity must decrease ($\omega_f < \omega_i$) to keep the angular momentum constant.