Question

The rod AB of length $l$ and mass m can rotate freely about A in a vertical plane. A point mass m is attached to the other end of the rod and the system is released from its horizontal position. The initial angular acceleration is

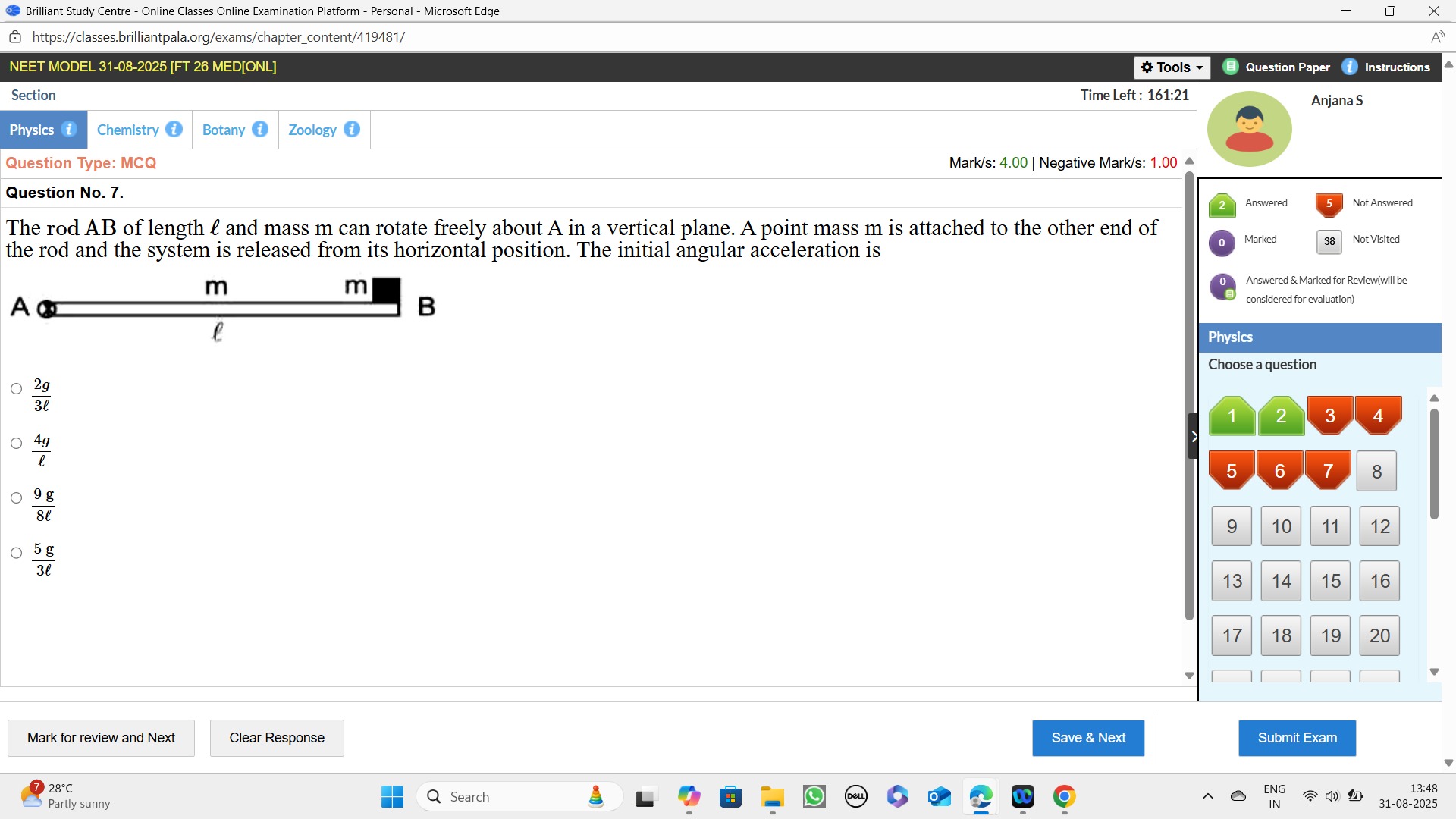
• A. $\frac{2g}{3l}$
• B. $\frac{4g}{l}$
• C. $\frac{9g}{8l}$
• D. $\frac{5g}{3l}$

Answer 1

Answer: (C)

$\frac{9g}{8l}$

Answer 2

The system consists of a rod of mass $m$ and length $l$, pivoted at end A, and a point mass $m$ attached at end B. The system is released from a horizontal position.

1. Torque Calculation:

   • The gravitational force on the rod ($mg$) acts at its center of mass, which is at a distance $l/2$ from the pivot A. The torque due to the rod is $\tau_{rod} = (mg) \times (l/2)$.
   • The gravitational force on the point mass ($mg$) acts at end B, which is at a distance $l$ from the pivot A. The torque due to the point mass is $\tau_{mass} = (mg) \times l$.
   • Since the system is released from the horizontal position, both forces create torques in the same direction (clockwise). The total torque about A is $\tau_{total} = \tau_{rod} + \tau_{mass} = \frac{mgl}{2} + mgl = \frac{3mgl}{2}$.

2. Moment of Inertia Calculation:

   • The moment of inertia of the rod about end A is $I_{rod} = \frac{1}{3}ml^2$.
   • The moment of inertia of the point mass $m$ at end B (distance $l$ from A) about A is $I_{mass} = m \times l^2$.
   • The total moment of inertia of the system about A is $I_{total} = I_{rod} + I_{mass} = \frac{1}{3}ml^2 + ml^2 = \frac{4}{3}ml^2$.

3. Angular Acceleration Calculation:

   • Using Newton's second law for rotation, $\tau_{total} = I_{total} \alpha$, where $\alpha$ is the initial angular acceleration.
   • $\frac{3mgl}{2} = \left(\frac{4}{3}ml^2\right) \alpha$
   • Solving for $\alpha$: $\alpha = \frac{\frac{3mgl}{2}}{\frac{4ml^2}{3}} = \frac{3}{2} \times \frac{3}{4} \times \frac{mg}{ml} \times \frac{l}{l} = \frac{9g}{8l}$