Question
Question: The value of $K_c$ is 64 at 800 K for the reaction: $N_2 + 3H_2 \rightleftharpoons 2NH_3$ (all gases...
The value of Kc is 64 at 800 K for the reaction: N2+3H2⇌2NH3 (all gases). Therefore the value of Kc at 800 K for the reaction NH3⇌21N2+23H2 (all gases) is
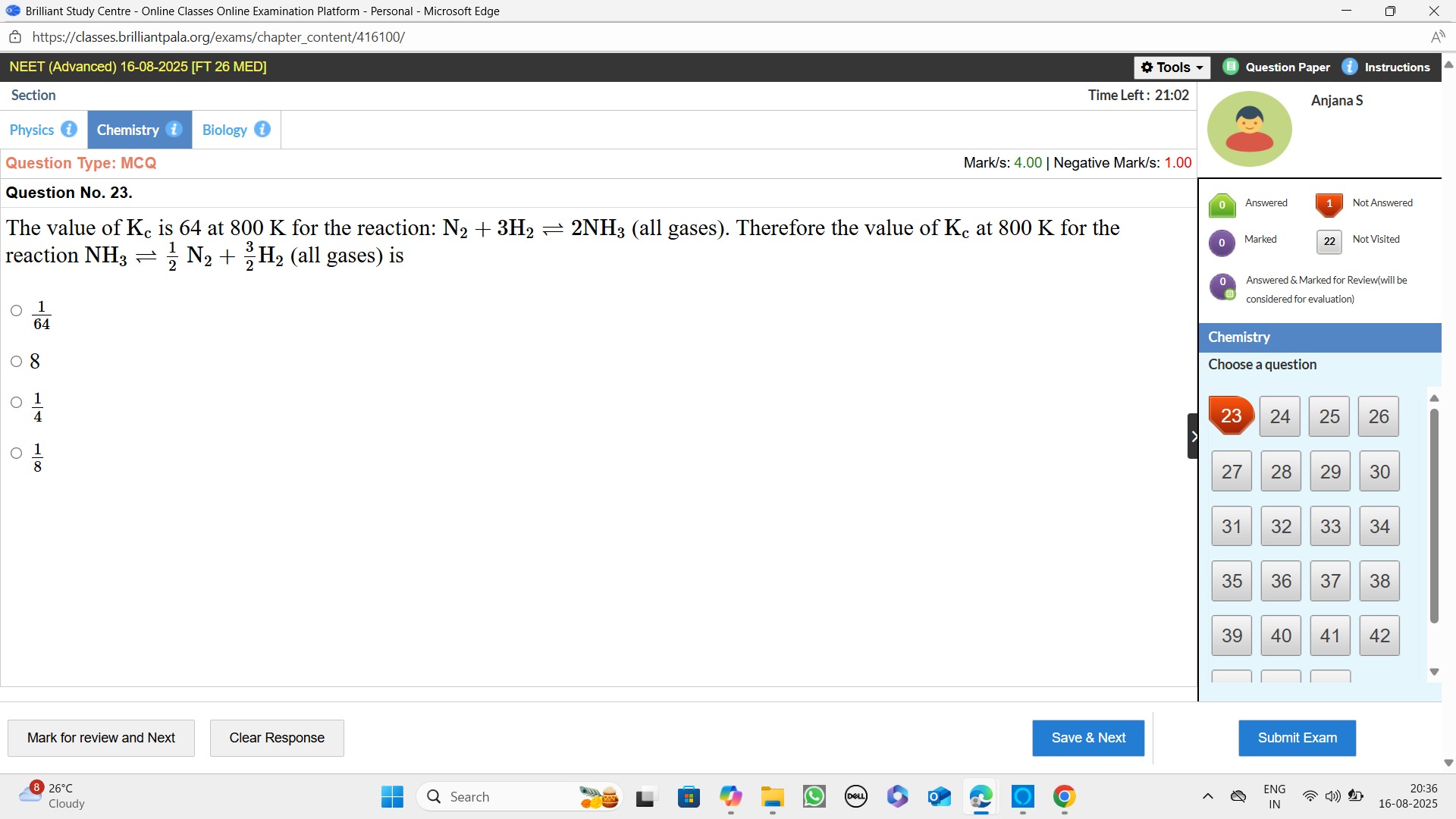
641
8
41
81
81
Solution
To find the value of Kc for the reaction NH3⇌21N2+23H2, we need to relate it to the given reaction N2+3H2⇌2NH3.
Let the given reaction be (1):
N2(g)+3H2(g)⇌2NH3(g)
The equilibrium constant for reaction (1) is Kc1=64. The expression for Kc1 is:
Kc1=[N2][H2]3[NH3]2=64
Let the target reaction be (2):
NH3(g)⇌21N2(g)+23H2(g)
We need to find Kc2. The expression for Kc2 is:
Kc2=[NH3][N2]1/2[H2]3/2
Comparing reaction (2) with reaction (1), we can observe two changes:
- Reaction (2) is the reverse of reaction (1).
- The stoichiometric coefficients of reaction (2) are half of the stoichiometric coefficients of the reverse of reaction (1).
Step 1: Reverse reaction (1).
If a reaction is reversed, the new equilibrium constant is the reciprocal of the original equilibrium constant. Let's reverse reaction (1) to get reaction (1'):
2NH3(g)⇌N2(g)+3H2(g)
The equilibrium constant for reaction (1'), Kc1′, will be:
Kc1′=Kc11=641
Step 2: Divide the stoichiometric coefficients of reaction (1') by 2.
If the stoichiometric coefficients of a reaction are multiplied by a factor 'n', the new equilibrium constant is the original equilibrium constant raised to the power 'n'. In this case, we are multiplying by n=21 (which is equivalent to taking the square root).
Reaction (2) is obtained by multiplying reaction (1') by 21:
21(2NH3(g)⇌N2(g)+3H2(g))
This gives:
NH3(g)⇌21N2(g)+23H2(g)
The equilibrium constant for reaction (2), Kc2, will be:
Kc2=(Kc1′)1/2
Kc2=(641)1/2
Kc2=641
Kc2=641
Kc2=81
The value of Kc at 800 K for the reaction NH3⇌21N2+23H2 is 81.
