Question
Question: Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on...
Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero.
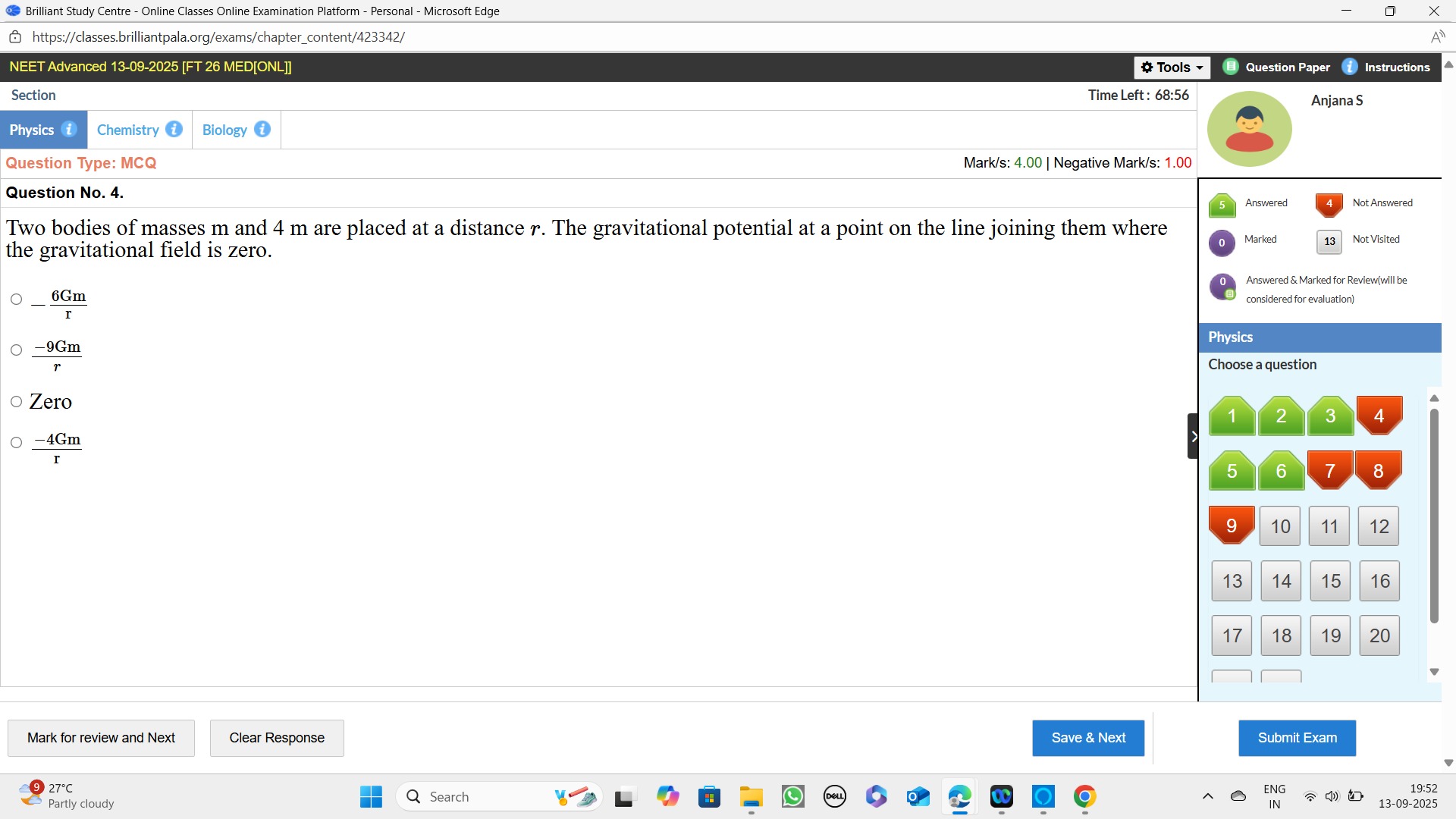
r6Gm
r−9Gm
Zero
r−4Gm
r−9Gm
Solution
Let the two masses be m and 4m placed at a distance r. Let the point where the gravitational field is zero be at a distance x from mass m. Then its distance from mass 4m is (r−x). For the gravitational field to be zero, the point must lie between the two masses.
The gravitational field due to mass m at this point is E1=x2Gm. The gravitational field due to mass 4m at this point is E2=(r−x)2G(4m).
For the net gravitational field to be zero, their magnitudes must be equal: x2Gm=(r−x)2G(4m) x21=(r−x)24 Taking the square root of both sides: x1=r−x2(since x and r−x are positive) r−x=2x r=3x x=3r The distance of the point from mass 4m is r−x=r−3r=32r.
The gravitational potential at this point is the sum of the potentials due to each mass: V=Vm+V4m V=−xGm−r−xG(4m) Substitute the values of x and r−x: V=−r/3Gm−2r/3G(4m) V=−r3Gm−2r4Gm×3 V=−r3Gm−2r12Gm V=−r3Gm−r6Gm V=−r9Gm
