Solveeit Logo
Login

Question

Question: Masses M, m, m and m are placed at points A, B, C and D of an equilateral triangle ABC. A, B and C b...

Masses M, m, m and m are placed at points A, B, C and D of an equilateral triangle ABC. A, B and C being the corners and D being the midpoint of BC. If the net field at the at the centroid is zero, then

A

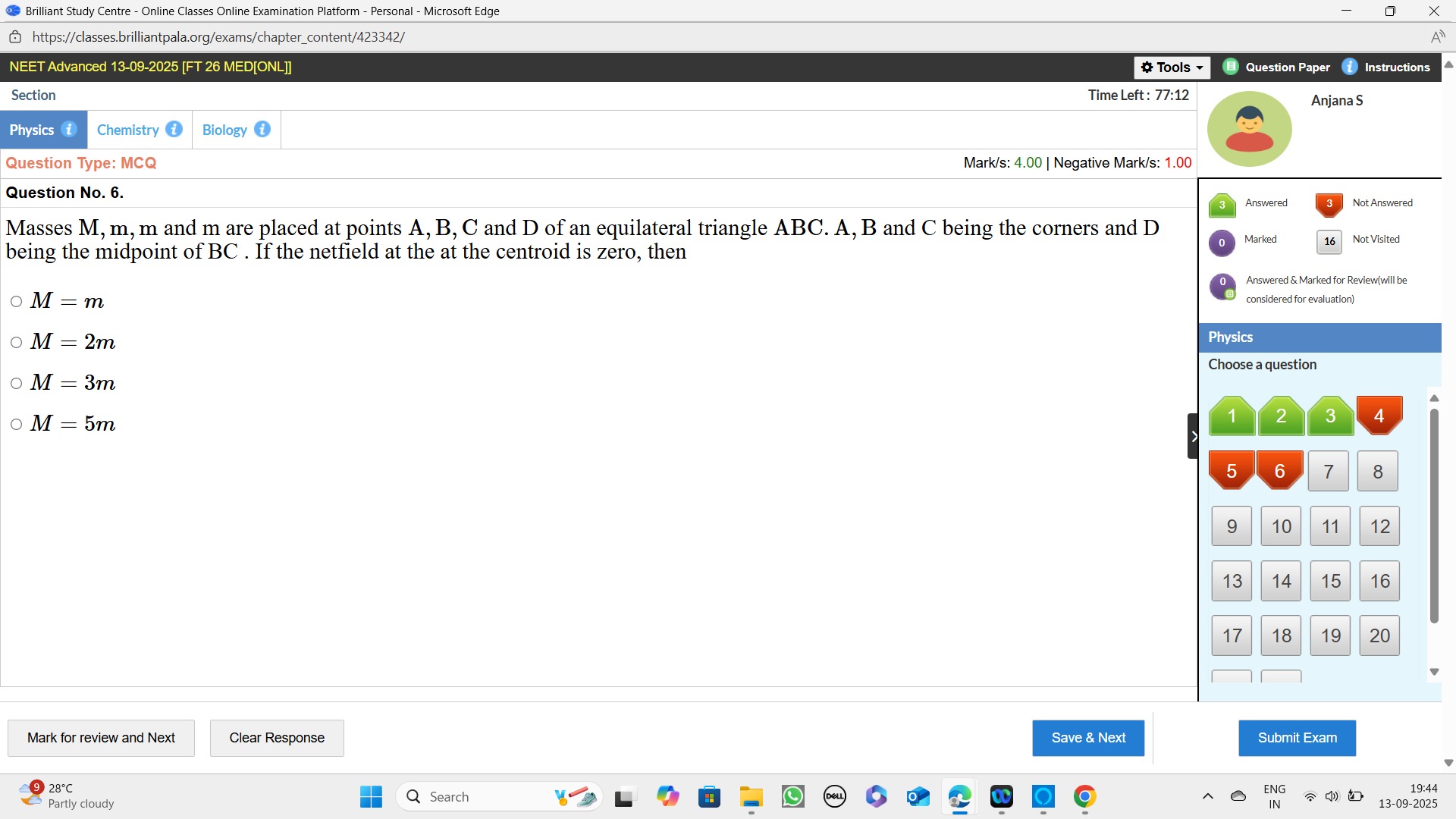
M = m

B

M = 2m

C

M = 3m

D

M = 5m

Answer

M = 5m

Explanation

Solution

Let G be the centroid of the equilateral triangle ABC. Let the origin of our coordinate system be at G. For an equilateral triangle, the centroid is equidistant from its vertices. Let this distance be RR. The distance from the centroid to the midpoint of a side is R/2R/2. Let D be the midpoint of BC.

The position vectors of the vertices A, B, C from the centroid G satisfy r⃗A+r⃗B+r⃗C=0⃗\vec{r}_A + \vec{r}_B + \vec{r}_C = \vec{0}. The position vector of D, the midpoint of BC, is r⃗D=r⃗B+r⃗C2\vec{r}_D = \frac{\vec{r}_B + \vec{r}_C}{2}. Substituting r⃗B+r⃗C=−r⃗A\vec{r}_B + \vec{r}_C = -\vec{r}_A, we get r⃗D=−r⃗A2\vec{r}_D = -\frac{\vec{r}_A}{2}. This implies that r⃗A\vec{r}_A and r⃗D\vec{r}_D are collinear and point in opposite directions, with ∣r⃗D∣=∣r⃗A∣/2|\vec{r}_D| = |\vec{r}_A|/2.

The gravitational field at the centroid G due to a mass mim_i at position r⃗i\vec{r}_i is given by E⃗i=−Gmi∣r⃗i∣3r⃗i\vec{E}_i = -G \frac{m_i}{|\vec{r}_i|^3} \vec{r}_i (where r⃗i\vec{r}_i is the position vector from the mass to the point G).

The masses are M at A, m at B, m at C, and m at D. The net field at G is zero. E⃗net=E⃗A+E⃗B+E⃗C+E⃗D=0⃗\vec{E}_{net} = \vec{E}_A + \vec{E}_B + \vec{E}_C + \vec{E}_D = \vec{0}.

The distances from G to A, B, C are all RR. The distance from G to D is R/2R/2. E⃗A=−GMR3r⃗A\vec{E}_A = -G \frac{M}{R^3} \vec{r}_A E⃗B=−GmR3r⃗B\vec{E}_B = -G \frac{m}{R^3} \vec{r}_B E⃗C=−GmR3r⃗C\vec{E}_C = -G \frac{m}{R^3} \vec{r}_C E⃗D=−Gm(R/2)3r⃗D=−G8mR3r⃗D\vec{E}_D = -G \frac{m}{(R/2)^3} \vec{r}_D = -G \frac{8m}{R^3} \vec{r}_D

Summing these fields and setting to zero: −GMR3r⃗A−GmR3r⃗B−GmR3r⃗C−G8mR3r⃗D=0⃗-G \frac{M}{R^3} \vec{r}_A - G \frac{m}{R^3} \vec{r}_B - G \frac{m}{R^3} \vec{r}_C - G \frac{8m}{R^3} \vec{r}_D = \vec{0} Multiplying by −R3G-\frac{R^3}{G}: Mr⃗A+mr⃗B+mr⃗C+8mr⃗D=0⃗M \vec{r}_A + m \vec{r}_B + m \vec{r}_C + 8m \vec{r}_D = \vec{0} Mr⃗A+m(r⃗B+r⃗C)+8mr⃗D=0⃗M \vec{r}_A + m(\vec{r}_B + \vec{r}_C) + 8m \vec{r}_D = \vec{0} Substitute r⃗B+r⃗C=−r⃗A\vec{r}_B + \vec{r}_C = -\vec{r}_A: Mr⃗A+m(−r⃗A)+8mr⃗D=0⃗M \vec{r}_A + m(-\vec{r}_A) + 8m \vec{r}_D = \vec{0} (M−m)r⃗A+8mr⃗D=0⃗(M-m)\vec{r}_A + 8m\vec{r}_D = \vec{0} Substitute r⃗D=−r⃗A2\vec{r}_D = -\frac{\vec{r}_A}{2}: (M−m)r⃗A+8m(−r⃗A2)=0⃗(M-m)\vec{r}_A + 8m(-\frac{\vec{r}_A}{2}) = \vec{0} (M−m)r⃗A−4mr⃗A=0⃗(M-m)\vec{r}_A - 4m\vec{r}_A = \vec{0} (M−m−4m)r⃗A=0⃗(M-m-4m)\vec{r}_A = \vec{0} (M−5m)r⃗A=0⃗(M-5m)\vec{r}_A = \vec{0} Since r⃗A\vec{r}_A is a non-zero vector (pointing from G to A), the coefficient must be zero: M−5m=0  ⟹  M=5mM-5m = 0 \implies M = 5m.