Question
Question: An electric dipole is placed at distance x from an infinitely long rod of linear charge density $\la...
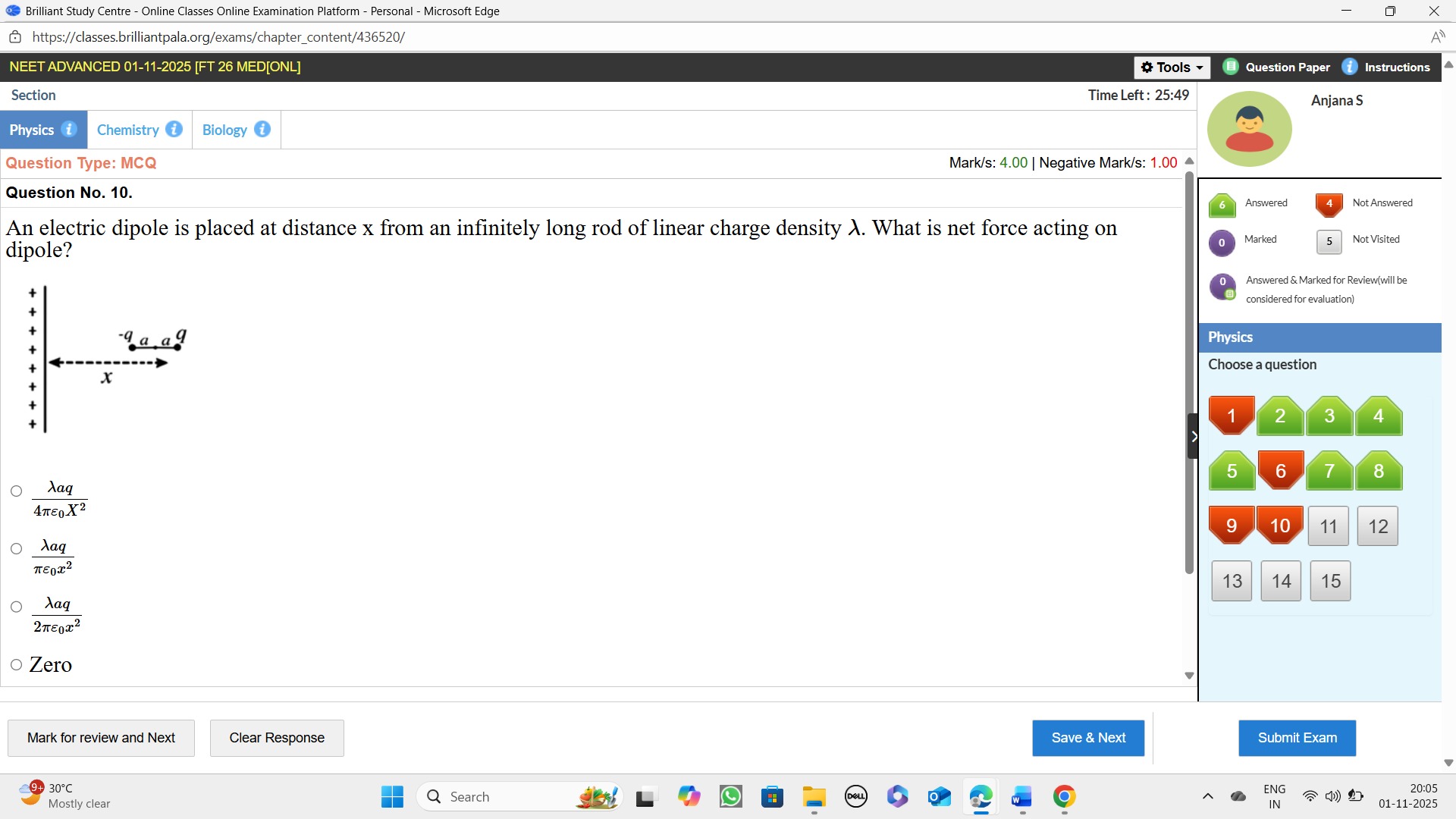
An electric dipole is placed at distance x from an infinitely long rod of linear charge density λ. What is net force acting on dipole?
A
4πϵ0X2λaq
B
πϵ0x2λaq
C
2πϵ0x2λaq
D
Zero
Answer
πϵ0x2λaq
Explanation
Solution
The electric field at a distance r from an infinitely long rod with linear charge density λ is E(r)=2πϵ0rλ. For a dipole with charges −q and +q separated by 2a, at distances x−a and x+a from the rod, the net force is: Fnet=(−q)E(x−a)+(+q)E(x+a) Fnet=−q2πϵ0(x−a)λ+q2πϵ0(x+a)λ Fnet=2πϵ0λq(x+a1−x−a1) Fnet=2πϵ0λq((x+a)(x−a)(x−a)−(x+a))=2πϵ0λq(x2−a2−2a) For a≪x, Fnet≈−2πϵ0x22aλq=−πϵ0x2aλq. The magnitude is πϵ0x2aλq.
