Question
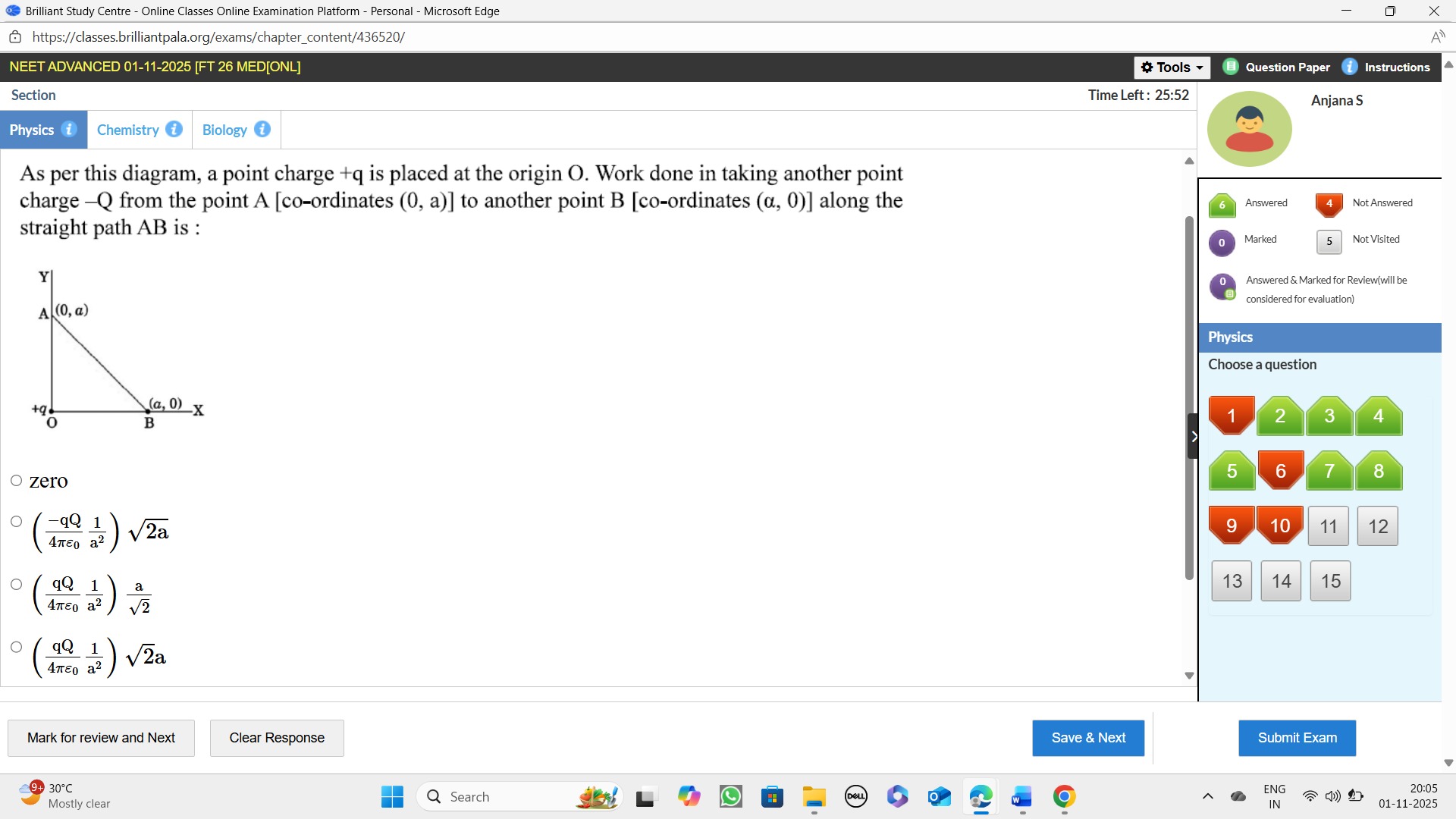
Question: As per this diagram, a point charge +q is placed at the origin O. Work done in taking another point ...
As per this diagram, a point charge +q is placed at the origin O. Work done in taking another point charge -Q from the point A [co-ordinates (0, a)] to another point B [co-ordinates (a, 0)] along the straight path AB is :
zero
4πϵ0−qQa212a
4πϵ0qQa212a
(4πϵ0qQa21)2a
zero
Solution
The work done in moving a charge in an electrostatic field is path-independent and depends only on the initial and final points. The work done by an external agent is given by Wext=qtest(VB−VA).
The distance of point A (0, a) from the origin (0, 0) is rA=(0−0)2+(a−0)2=a. The distance of point B (a, 0) from the origin (0, 0) is rB=(a−0)2+(0−0)2=a.
The electric potential at a distance r from a point charge q′ is V=4πϵ01rq′. The potential at A due to +q at the origin is VA=4πϵ01aq. The potential at B due to +q at the origin is VB=4πϵ01aq.
Since VA=VB, the potential difference VB−VA=0. The work done in moving charge -Q from A to B is Wext=(−Q)(VB−VA)=(−Q)(0)=0.
