Question

An electric field $\overrightarrow{E} = 2x\hat{i} + 3\hat{j} – 4\hat{k}$ exist in a region. A cube of side $2m$ is imagined in the region as shown. Then flux through the right face, top face and front face are respectively in Vm

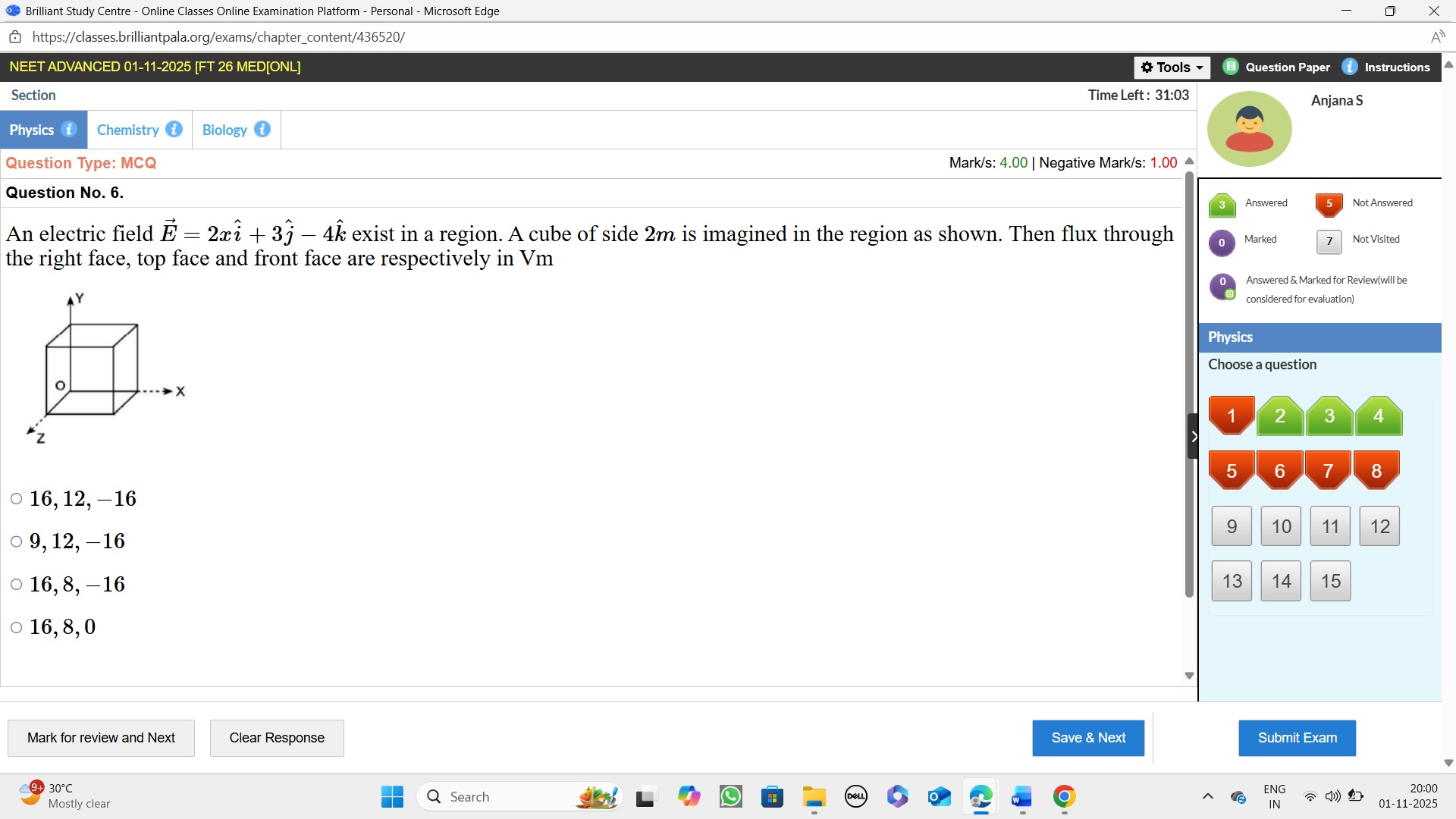
• A. 16, 12, -16
• B. 9, 12, -16
• C. 16, 8, -16
• D. 16, 8, 0

Answer 1

Answer: (A)

16, 12, -16

Answer 2

Flux through the right face (at $x=2$): $\overrightarrow{E}(x=2) = 4\hat{i} + 3\hat{j} - 4\hat{k}$. Area vector $\overrightarrow{A}_{right} = (2 \times 2)\hat{i} = 4\hat{i}$. Flux $\Phi_{right} = \overrightarrow{E} \cdot \overrightarrow{A}_{right} = (4\hat{i} + 3\hat{j} - 4\hat{k}) \cdot (4\hat{i}) = 16 \text{ Vm}$.

Flux through the top face (at $y=2$): The electric field component normal to this face is $E_y = 3$. Area vector $\overrightarrow{A}_{top} = (2 \times 2)\hat{j} = 4\hat{j}$. Flux $\Phi_{top} = E_y \times \text{Area} = 3 \times (2 \times 2) = 12 \text{ Vm}$.

Flux through the front face (at $z=2$): The electric field component normal to this face is $E_z = -4$. Area vector $\overrightarrow{A}_{front} = (2 \times 2)\hat{k} = 4\hat{k}$. Flux $\Phi_{front} = E_z \times \text{Area} = -4 \times (2 \times 2) = -16 \text{ Vm}$.