Question
Question: A uniform rod is hinged as shown and is released from a horizontal position. The angular velocity of...
A uniform rod is hinged as shown and is released from a horizontal position. The angular velocity of the rod as it passes the vertical position (neglect friction)
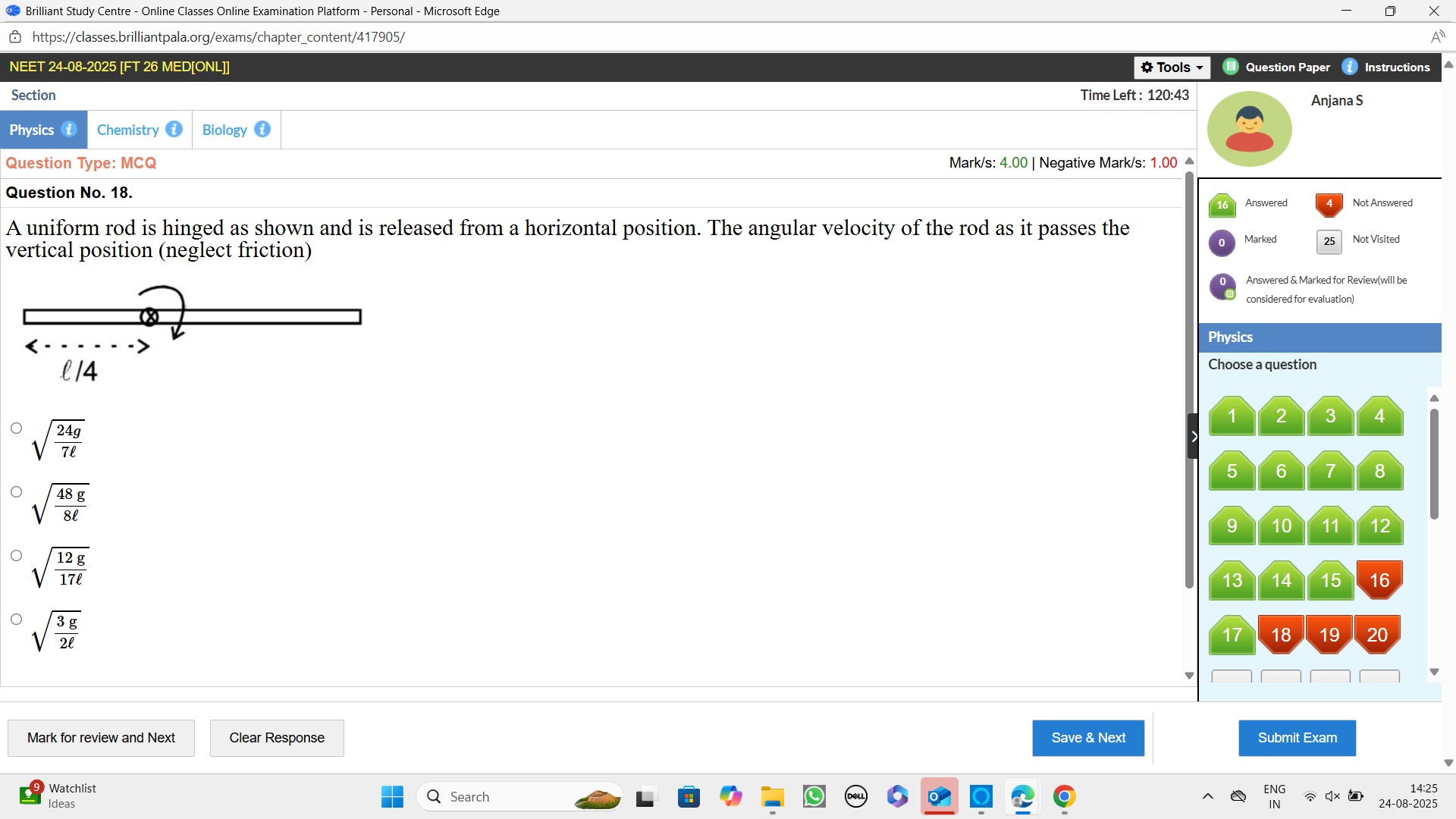
7l24g
8l48g
17ℓ12g
2l3g
7l24g
Solution
To determine the angular velocity of the rod as it passes the vertical position, we use the principle of conservation of mechanical energy.
1. Define Initial and Final States:
-
Initial State (Horizontal Position, released from rest):
- Let the hinge be the reference level for potential energy (PE = 0).
- The center of mass (CM) of the uniform rod is at its geometric center,
l/2from either end. The hinge is atl/4from one end. Therefore, the distance of the CM from the hinge isd = l/2 - l/4 = l/4. - In the horizontal position, the CM is at the same height as the hinge.
- Initial Potential Energy (PEi) =
0. - Initial Kinetic Energy (KEi) =
0(since it's released from rest). - Total Initial Energy (Ei) = PEi+KEi=0.
-
Final State (Vertical Position):
- When the rod is vertical, the CM is now
l/4below the hinge. - Final Potential Energy (PEf) =
-mg(l/4). - Final Kinetic Energy (KEf) =
(1/2)I_hinge ω², whereI_hingeis the moment of inertia about the hinge andωis the angular velocity. - Total Final Energy (Ef) = PEf+KEf=−mg(l/4)+(1/2)Ihingeω2.
- When the rod is vertical, the CM is now
2. Calculate the Moment of Inertia about the Hinge (Ihinge):
-
The moment of inertia of a uniform rod of mass
mand lengthlabout its center of mass (ICM) is(1/12)ml². -
Using the parallel axis theorem, the moment of inertia about the hinge (which is at a distance
d = l/4from the CM) is:Ihinge=ICM+md2
Ihinge=(1/12)ml2+m(l/4)2
Ihinge=(1/12)ml2+m(l2/16)
To add these, find a common denominator (48):
Ihinge=(4/48)ml2+(3/48)ml2
Ihinge=(7/48)ml2
3. Apply Conservation of Mechanical Energy:
-
Since friction is neglected, mechanical energy is conserved: Ei=Ef.
-
0=−mg(l/4)+(1/2)Ihingeω2
-
Rearrange the equation:
mg(l/4)=(1/2)Ihingeω2
4. Substitute Ihinge and Solve for ω:
-
mg(l/4)=(1/2)∗(7/48)ml2∗ω2
-
Cancel mass
mfrom both sides:g(l/4)=(1/2)∗(7/48)l2∗ω2
-
Cancel one
lfrom both sides (assumingl ≠ 0):g/4=(1/2)∗(7/48)l∗ω2
-
Multiply both sides by 2:
g/2=(7/48)l∗ω2
-
Isolate ω2:
ω2=(g/2)∗(48/(7l))
ω2=(g∗48)/(2∗7l)
ω2=(g∗24)/(7l)
ω2=7l24g
-
Take the square root to find ω:
ω=7l24g
The final answer is 7l24g.
Explanation of the solution:
- Energy Conservation: The rod is released from rest in a horizontal position. As it swings to the vertical position, its potential energy is converted into rotational kinetic energy.
- Potential Energy Change: The center of mass (CM) of the rod moves from the hinge level (initial PE = 0) to a distance
l/4below the hinge (final PE =-mg(l/4)). The loss in potential energy ismg(l/4). - Rotational Kinetic Energy: The gain in kinetic energy is
(1/2)Iω², whereIis the moment of inertia about the hinge andωis the angular velocity. - Moment of Inertia: For a uniform rod, ICM=(1/12)ml2. The hinge is at
l/4from the CM. By the parallel axis theorem, Ihinge=ICM+m(l/4)2=(1/12)ml2+(1/16)ml2=(7/48)ml2. - Equating Energies:
mg(l/4) = (1/2) * (7/48)ml² * ω². - Solve for ω: Simplifying the equation yields
ω = \sqrt{\frac{24g}{7l}}.
Answer:
The correct option is 7l24g.
