Question

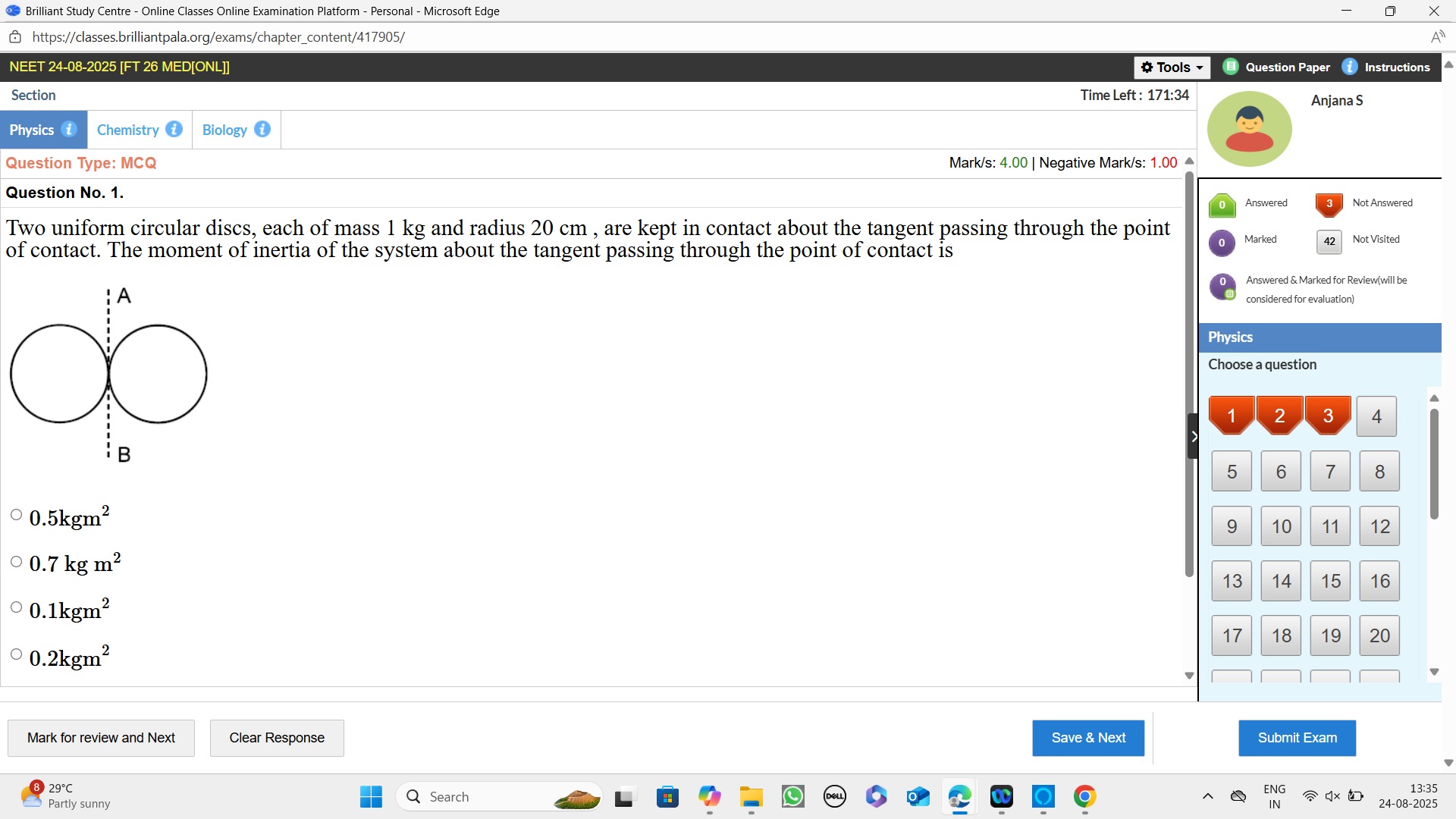
Two uniform circular discs, each of mass 1 kg and radius 20 cm, are kept in contact about the tangent passing through the point of contact. The moment of inertia of the system about the tangent passing through the point of contact is

• A. 0.5kgm²
• B. 0.7 kg m²
• C. 0.1kgm²
• D. 0.2kgm²

Answer 1

Answer: (C)

0.1 kg m²

Answer 2

The problem asks for the moment of inertia of a system of two uniform circular discs about a tangent passing through their point of contact.

1. Moment of Inertia of a Single Disc about a Diameter:

For a uniform circular disc of mass $M$ and radius $R$, the moment of inertia about an axis passing through its center and perpendicular to its plane is $I_c = \frac{1}{2}MR^2$.

According to the Perpendicular Axis Theorem, for a planar lamina, $I_z = I_x + I_y$. For a circular disc, due to symmetry, the moment of inertia about any diameter is the same. Let this be $I_d$. So, $I_z = I_d + I_d = 2I_d$.

Therefore, the moment of inertia about a diameter is: $I_d = \frac{I_c}{2} = \frac{1}{2} \left( \frac{1}{2}MR^2 \right) = \frac{1}{4}MR^2$.

2. Moment of Inertia of a Single Disc about the Given Tangent (Axis AB):

The axis AB is a tangent to each disc and lies in the plane of the disc. This axis is parallel to a diameter of each disc. The distance from the center of each disc to the axis AB is equal to its radius, $R$.

Using the Parallel Axis Theorem, $I = I_{CM} + Md^2$, where $I_{CM}$ is the moment of inertia about an axis passing through the center of mass (which is $I_d$ in this case) and $d$ is the perpendicular distance between the two parallel axes (which is $R$).

So, for one disc, the moment of inertia about the tangent AB is: $I_{disc} = I_d + MR^2 = \frac{1}{4}MR^2 + MR^2 = \frac{5}{4}MR^2$.

3. Moment of Inertia of the System:

The system consists of two identical discs. The axis AB is a common tangent to both discs. The total moment of inertia of the system is the sum of the moments of inertia of the individual discs about the axis AB. $I_{system} = I_{disc1} + I_{disc2}$

Since both discs are identical and the axis is a tangent to both, $I_{disc1} = I_{disc2} = \frac{5}{4}MR^2$.

$I_{system} = \frac{5}{4}MR^2 + \frac{5}{4}MR^2 = 2 \times \frac{5}{4}MR^2 = \frac{5}{2}MR^2$.

4. Calculation with Given Values:

Given: Mass of each disc, $M = 1$ kg Radius of each disc, $R = 20$ cm $= 0.2$ m

Substitute these values into the formula for $I_{system}$: $I_{system} = \frac{5}{2} \times (1 \text{ kg}) \times (0.2 \text{ m})^2$ $I_{system} = \frac{5}{2} \times 1 \times 0.04 \text{ kg m}^2$ $I_{system} = 5 \times 0.02 \text{ kg m}^2$ $I_{system} = 0.1 \text{ kg m}^2$

The final answer is $\boxed{\text{0.1kgm²}}$.

Explanation of the solution:

1. Moment of inertia of a disc about a diameter: $I_d = \frac{1}{4}MR^2$.
2. Moment of inertia of one disc about the tangent AB: Using the Parallel Axis Theorem, $I_{disc} = I_d + MR^2 = \frac{1}{4}MR^2 + MR^2 = \frac{5}{4}MR^2$.
3. Moment of inertia of the system: Since the system has two identical discs and the axis AB is a tangent to both, $I_{system} = 2 \times I_{disc} = 2 \times \frac{5}{4}MR^2 = \frac{5}{2}MR^2$.
4. Substitute values: $M=1$ kg, $R=0.2$ m. $I_{system} = \frac{5}{2} \times 1 \times (0.2)^2 = \frac{5}{2} \times 0.04 = 5 \times 0.02 = 0.1 \text{ kg m}^2$.