Question
Question: A block of wood of mass 3 M is suspended by a string of length $\frac{10}{3}$ m. A bullet of mass M ...
A block of wood of mass 3 M is suspended by a string of length 310 m. A bullet of mass M hits it with a certain velocity and gets embedded in it. The block and the bullet swing to one side till the string makes 120° with the initial position. The velocity of the bullet is (g=10 ms−2)
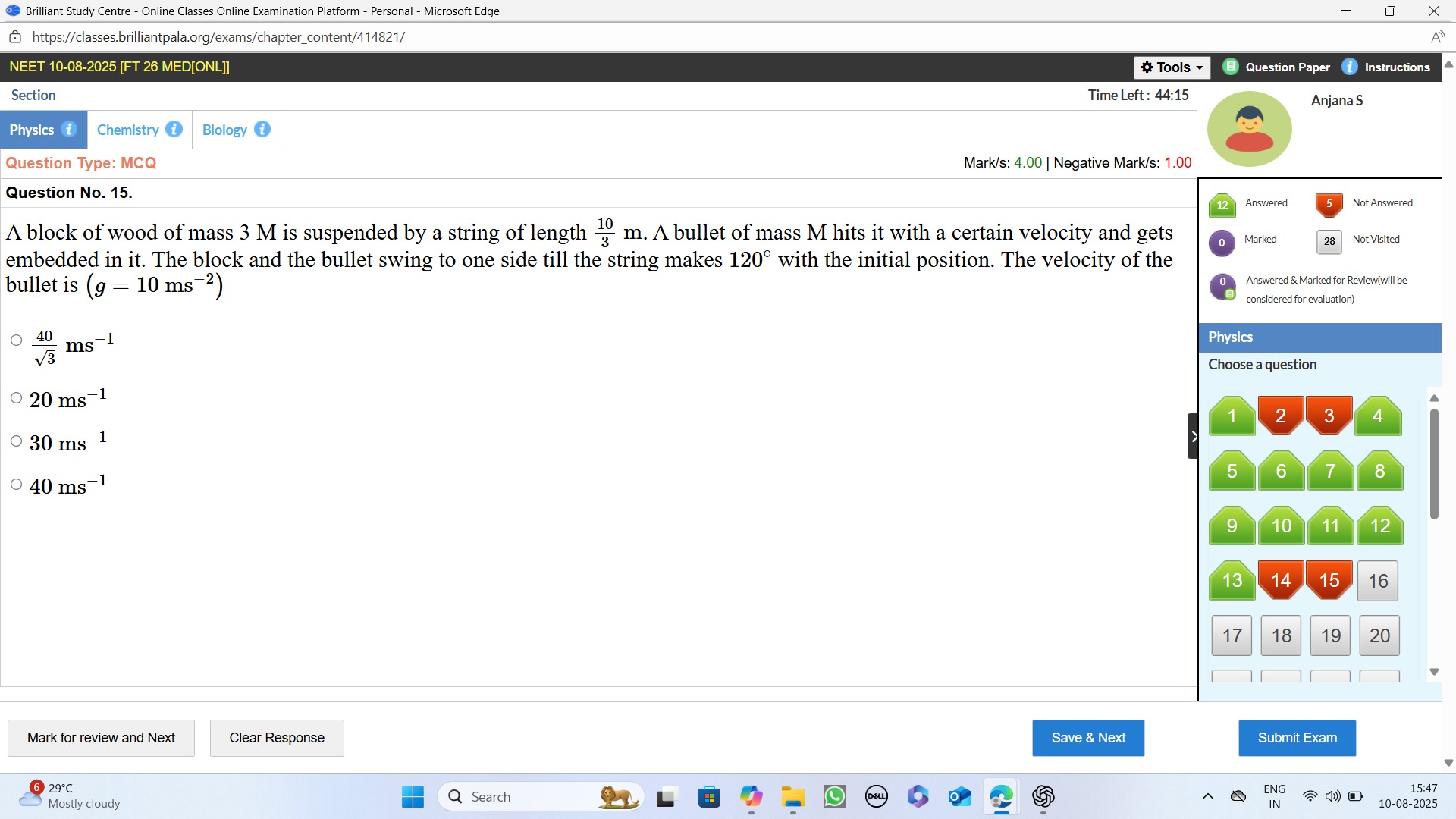
340 ms−1
20 ms−1
30 ms−1
40 ms−1
The velocity of the bullet is 40 ms−1.
Solution
The problem involves two main stages: an inelastic collision followed by a pendulum swing.
Stage 1: Inelastic Collision
When the bullet hits the block and gets embedded, it's an inelastic collision. Linear momentum is conserved during this collision.
Let:
- Mass of bullet =
m_b = M - Initial velocity of bullet =
v(this is what we need to find) - Mass of block =
m_w = 3M - Initial velocity of block =
0 - Combined mass after collision =
m_c = m_b + m_w = M + 3M = 4M - Velocity of the combined system immediately after collision =
V
By conservation of linear momentum:
mbv+mw(0)=mcV
Mv=(4M)V
V=4v (Equation 1)
Stage 2: Pendulum Swing
After the collision, the combined block and bullet system swings upwards. During this swing, mechanical energy is conserved. The system starts with kinetic energy KE at the bottom and converts it into potential energy PE at the maximum height of the swing.
- Length of the string = L=310 m
- Angle made with the initial vertical position = θ=120°
- Acceleration due to gravity = g=10 ms−2
The vertical height h gained by the center of mass of the system can be calculated using the length of the string and the angle of swing:
h=L(1−cosθ)
Substitute the given values:
h=310(1−cos(120°))
We know that cos(120°)=−21.
h=310(1−(−21))
h=310(1+21)
h=310(23)
h=5 m
Now, apply conservation of mechanical energy:
Initial Kinetic Energy = Final Potential Energy
21mcV2=mcgh
21(4M)V2=(4M)gh
21V2=gh
V2=2gh
Substitute the value of h and g:
V2=2×10×5
V2=100
V=100
V=10 ms−1
Combining the stages:
Now, substitute the value of V back into Equation 1:
V=4v
10=4v
v=10×4
v=40 ms−1
The velocity of the bullet is 40 ms−1.
