Question
Question: A particle of mass = 1 kg lying on x -axis experience a force given by law F = x(3x - 2) Newton, whe...
A particle of mass = 1 kg lying on x -axis experience a force given by law F = x(3x - 2) Newton, where x is the x -coordinate of the particle in meters. What is the minimum speed to be imparted to the particle placed at x = 4 meters such that it reaches the origin.
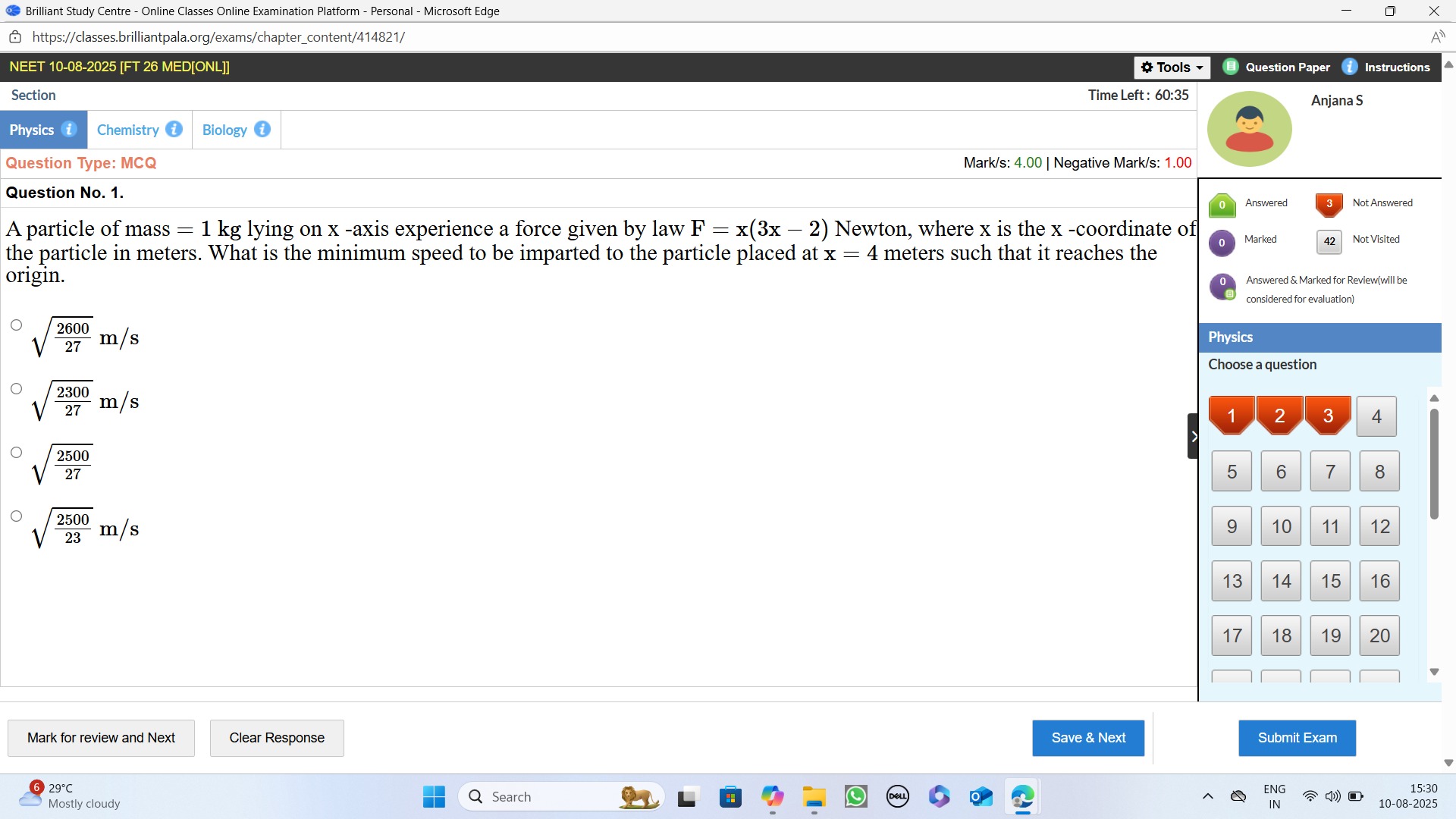
272600 m/s
272300 m/s
272500
232500 m/s
272600 m/s
Solution
The problem asks for the minimum speed to be imparted to a particle of mass m = 1 kg at x = 4 meters such that it reaches the origin (x = 0). The force acting on the particle is given by F = x(3x - 2) Newton.
-
Determine the potential energy function U(x): The force F is related to the potential energy U by the equation F = -dU/dx. So, dU = -F dx. Given F = x(3x² - 2x). Integrating to find U(x): U(x)=−∫(3x2−2x)dx U(x)=−(33x3−22x2)+C U(x)=−(x3−x2)+C We can set the integration constant C = 0, as only potential energy differences are physically significant. U(x)=x2−x3
-
Analyze the potential energy landscape: We need to find the potential energy at the initial position (x = 4), the final position (x = 0), and any critical points (local maxima or minima) between them. Critical points occur where F(x) = -dU/dx = 0. F(x)=x(3x−2)=0 This gives two critical points: x = 0 and x = 2/3.
Let's evaluate the potential energy at these points:
- At x = 0 (origin): U(0)=02−03=0
- At x = 2/3: U(2/3)=(2/3)2−(2/3)3=94−278=2712−278=274
- At x = 4 (initial position): U(4)=42−43=16−64=−48
Plotting these values or considering the second derivative of U(x) (or first derivative of F(x)) helps determine the nature of critical points. F(x) = 3x² - 2x. dF/dx = 6x - 2. At x = 0, dF/dx = -2 < 0, which means U(0) is a local minimum (stable equilibrium). At x = 2/3, dF/dx = 6(2/3) - 2 = 4 - 2 = 2 > 0, which means U(2/3) is a local maximum (unstable equilibrium).
The particle starts at x = 4 with U(4) = -48 J. It needs to reach x = 0 with U(0) = 0 J. On the path from x = 4 to x = 0, the particle must pass through the potential energy barrier at x = 2/3, where U(2/3) = 4/27 J. Since U(2/3) = 4/27 J is greater than both U(4) = -48 J and U(0) = 0 J, this point represents the highest potential energy the particle must overcome to reach the origin.
-
Apply the principle of conservation of mechanical energy: For the particle to reach the origin, its total mechanical energy (E = K + U) must be at least equal to the maximum potential energy it encounters on its path. For minimum initial speed, the kinetic energy at the peak of the barrier (x = 2/3) should be zero. Let v be the minimum speed imparted at x = 4. Initial energy E_initial = K_initial + U_initial = (1/2)mv² + U(4) Energy at the barrier E_barrier = K_barrier + U_barrier = 0 + U(2/3) (for minimum speed)
Setting E_initial = E_barrier: (1/2)mv2+U(4)=U(2/3) Given m = 1 kg: (1/2)(1)v2+(−48)=4/27 (1/2)v2=4/27+48 To sum the terms on the right: (1/2)v2=274+48×27 Calculate 48 × 27: 48×27=48×(30−3)=1440−144=1296 Substitute this value back: (1/2)v2=274+1296 (1/2)v2=271300 v2=272600 v=272600 m/s
This is the minimum speed required for the particle to cross the potential energy barrier at x = 2/3 and subsequently reach the origin.
