Question
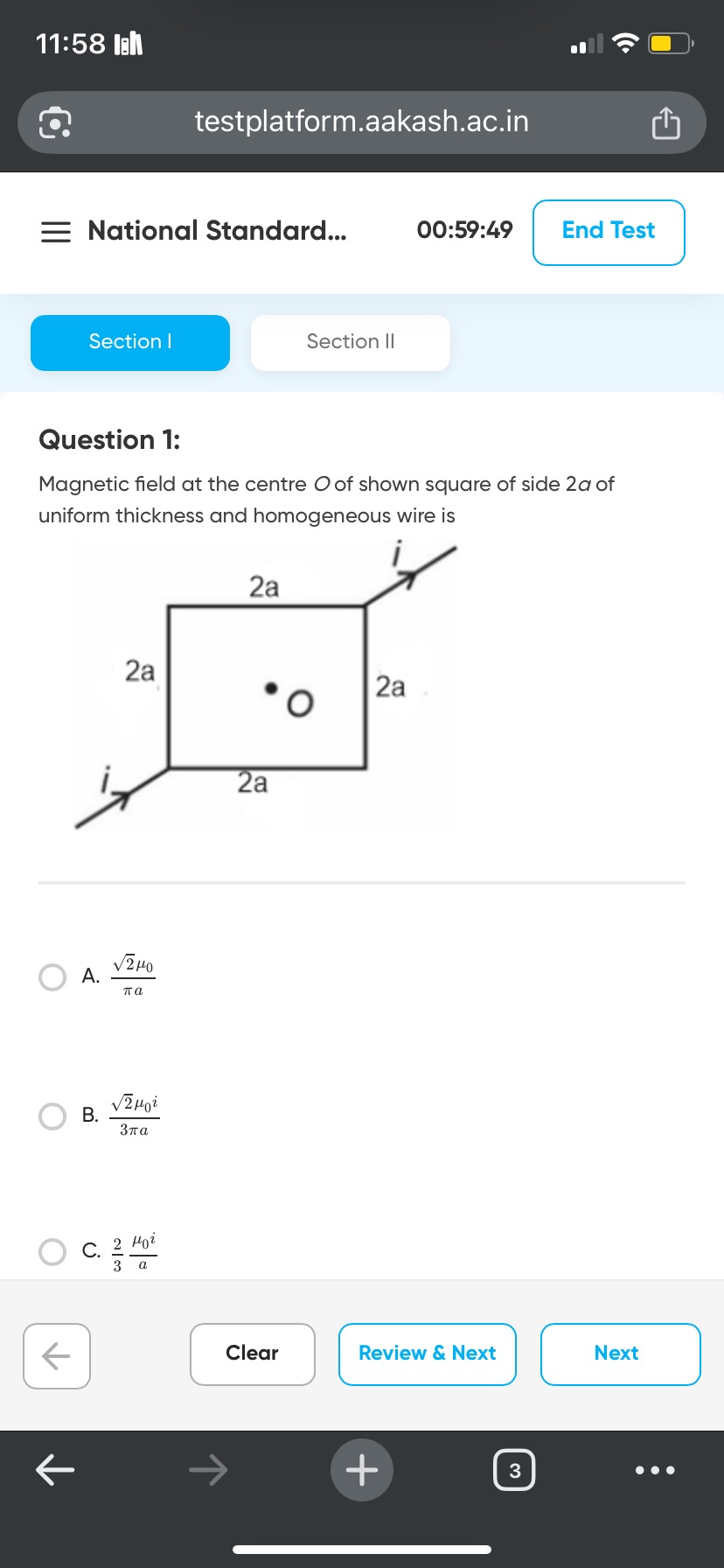
Question: Magnetic field at the centre O of shown square of side 2a of uniform thickness and homogeneous wire ...
Magnetic field at the centre O of shown square of side 2a of uniform thickness and homogeneous wire is
πa2μ0
3πa2μ0i
32aμ0i
πa2μ0
Solution
The problem asks for the magnetic field at the center O of a square loop of side 2a. A current 'i' enters at one corner and leaves at the diagonally opposite corner. The wire is stated to be of uniform thickness and homogeneous.
-
Current Distribution:
Let the corners of the square be A (bottom-left, where current enters), B (bottom-right), C (top-right, where current leaves), and D (top-left).
The current 'i' splits into two paths:- Path 1: A → B → C (ABC)
- Path 2: A → D → C (ADC)
Since the wire is uniform and homogeneous, the resistance of each segment is proportional to its length. Let the resistance of one side (length 2a) be R₀.
- Resistance of path ABC = R_AB + R_BC = R₀ + R₀ = 2R₀.
- Resistance of path ADC = R_AD + R_DC = R₀ + R₀ = 2R₀.
Since the resistances of the two paths are equal (2R0), the current 'i' will split equally into these two paths.
Therefore, the current in each path is i/2.- Current in segments AB and BC is iABC=i/2.
- Current in segments AD and DC is iADC=i/2.
-
Magnetic Field due to a Straight Wire Segment:
The magnetic field at a point due to a finite straight wire segment is given by:
B=4πdμ0I(sinθ1+sinθ2)
where I is the current, d is the perpendicular distance from the point to the wire, and θ1, θ2 are the angles subtended by the ends of the wire at the point with the perpendicular.For the center O of the square, the perpendicular distance 'd' to any side is half the side length, i.e., d=(2a)/2=a.
For any side of the square, the angles subtended at the center from its ends are 45∘ with the perpendicular. So, θ1=θ2=45∘.
Thus, the magnitude of the magnetic field at O due to any single side carrying current I is:
Bside=4πaμ0I(sin45∘+sin45∘)=4πaμ0I(21+21)=4πaμ0I22=22πaμ0I -
Direction of Magnetic Field using Right-Hand Rule:
Let's determine the direction of the magnetic field at O due to each segment using the right-hand thumb rule (thumb in current direction, fingers curl in B field direction).-
Segment AB: Current i/2 flows from A to B (rightwards). The center O is above this segment. So, the magnetic field BAB is into the page.
Magnitude: BAB=22πaμ0(i/2)=42πaμ0i. -
Segment BC: Current i/2 flows from B to C (upwards). The center O is to the left of this segment. So, the magnetic field BBC is into the page.
Magnitude: BBC=22πaμ0(i/2)=42πaμ0i. -
Segment CD: Current i/2 flows from D to C (rightwards). The center O is below this segment. So, the magnetic field BCD is out of the page.
Magnitude: BCD=22πaμ0(i/2)=42πaμ0i. -
Segment DA: Current i/2 flows from A to D (upwards). The center O is to the right of this segment. So, the magnetic field BDA is out of the page.
Magnitude: BDA=22πaμ0(i/2)=42πaμ0i.
-
-
Total Magnetic Field at O:
Let's assign 'into the page' as positive and 'out of the page' as negative.
Btotal=BAB+BBC+BCD+BDA
Btotal=(42πaμ0i)+(42πaμ0i)−(42πaμ0i)−(42πaμ0i)
Btotal=0The magnetic field at the center O is zero. This is a general result for a symmetrical current distribution in a uniform wire where current enters and leaves at diagonally opposite points of a regular polygon (like a square or circle).
-
Revisiting Options:
The calculated magnetic field is zero, but none of the given options are zero. This suggests a potential issue with the question or the options provided. However, if we are forced to choose from the given options, there might be an implicit assumption or a common misconception being tested.A common variant of this problem is finding the magnetic field at the center of a square loop carrying current 'i' around its entire perimeter. In that case, the total current in each side is 'i'.
If the current 'i' flowed entirely around the loop (e.g., clockwise), the magnetic field from all four sides would add up and be directed into the page.
For a square loop of side L = 2a carrying current I = i, the total magnetic field at the center is:
Bloop=4×Bside(I=i)=4×22πaμ0i=2πa2μ0i=πa2μ0iComparing this with the options: A. πa2μ0 (Missing 'i', dimensionally incorrect) B. 3πa2μ0i C. 32aμ0i
If option A was meant to be πa2μ0i, it would perfectly match the calculation for a full square loop carrying current 'i'. Given the context of competitive exams, sometimes questions are posed where the diagram might be misleading or there's a typo in options. If the intended question was a simple square loop with current 'i' flowing around it, then option A (with 'i' added) would be the answer.
However, strictly based on the diagram and "uniform thickness and homogeneous wire", the field should be zero. Since zero is not an option, and option A is dimensionally incorrect, there's a high probability of an error in the question or options.
If we assume that the question implies a common mistake or a non-standard interpretation, it becomes speculative. But based on standard physics principles, the field is zero.
Let's re-examine if there's any scenario where one of the given options could be correct.
Perhaps the question is from a specific context where 'i' refers to current in a segment, but that contradicts the input/output arrows.Given the options, and the common type of question, it's highly probable that Option A is the intended answer, assuming a typo where 'i' is missing and the diagram is misinterpreted as a full loop of current 'i'. But this is a strong assumption.
Let's consider the possibility that the problem is not about a square loop but part of a larger circuit where the current 'i' is the total current entering and leaving the square.
If we strictly follow the problem statement and diagram, the magnetic field at the center is zero. Since zero is not an option, and Option A is dimensionally incorrect as written, the question is flawed. However, in multiple choice questions, sometimes the "closest" or "most likely intended" answer is expected. If Option A was πa2μ0i, it would be the answer for a full square loop.
Given the choices, and the fact that option A is dimensionally incorrect (missing 'i'), there might be a typo in option A and it should have been πa2μ0i. If it was, it would be the field for a current 'i' flowing around the entire loop, which is a common problem. If the problem setters made a mistake in the diagram and intended a simple current loop, then A would be the answer.
Without further clarification or correction, the question is ambiguous due to the discrepancy between the derived answer (zero) and the provided options. If we must choose, and assuming a typo in option A, and a misrepresentation in the diagram (where 'i' is the current circulating in the loop), then A would be the answer.
However, if we strictly adhere to the diagram and the properties of the wire, the magnetic field is zero. Since zero is not an option, the problem is ill-posed. In such cases, one might infer the intended problem. The most standard problem related to this setup is a full square loop.
Let's assume there's a typo in option A and it should be πa2μ0i. And let's assume the diagram implies 'i' is the current flowing around the loop (ignoring the input/output points). This is a common interpretation in flawed questions.
Final check for the zero field:
The principle of superposition applies. The current 'i' splits into i/2 in path ABC and i/2 in path ADC.
The magnetic field due to path ABC (clockwise flow relative to O) would be into the page.
The magnetic field due to path ADC (counter-clockwise flow relative to O) would be out of the page.
Since both paths have equal current and are symmetrical, their contributions to the magnetic field at the center O will be equal in magnitude and opposite in direction, leading to a net magnetic field of zero.Since the options are non-zero, there's a high chance the question implicitly intends for a different scenario, or there's a mistake. If the question intended for the current 'i' to flow through the entire loop, then the magnetic field would be πa2μ0i. Given option A is πa2μ0, it is highly likely that 'i' was omitted due to a typo.
Given the context of JEE/NEET, sometimes questions test if a student recognizes the zero field condition. But if the options don't include zero, it's problematic.
Let's assume the question implicitly refers to a square loop with current 'i' flowing through it, and there's a typo in option A.
If the question is exactly as written and the options are exactly as written, then none of the options are correct. However, if forced to select, and assuming the common type of problem for a square loop, and a typo in option A.
Let's assume the student should recognize the zero field. If they don't, they might calculate for a full loop.
Given the options, and the common nature of such problems, it's plausible that the question intends to ask about a full loop with current 'i' and option A has a typo.
If the question is not flawed, and the answer is non-zero, it would imply unequal current distribution, which contradicts "uniform thickness and homogeneous wire".
Therefore, the most probable scenario is a flawed question where the intended answer is for a simple square loop carrying current 'i', and option A has a typo.
Let's provide the answer based on the interpretation that the question intended to ask for the magnetic field at the center of a square loop of side 2a carrying current 'i' around its perimeter, and that option A has a typo (missing 'i').
For a square loop of side L carrying current I, the magnetic field at the center is B=πL22μ0I.
Here, L = 2a and I = i.
B=π(2a)22μ0i=πa2μ0i.This matches option A if 'i' is added.
