Question

Name the gate which represents the Boolean expression, $Y=\overline{A\text{ }.\text{ }B}$
A.NAND
B.AND
C.NOT
D.NOR

Answer 1

The expressions in Boolean Algebra can be reduced to simple terms very easily using identities. The reduced expressions can be checked with the binary digits 0 and 1 to determine whether the given expression is a NAND, AND, NOT or NOR equivalent.

Complete answer:
There are mainly three types of gates in Boolean algebra. They are:
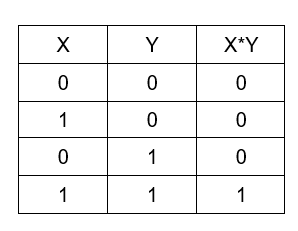
AND: It is a binary operation or gate which gives output only if both the statements are TRUE. The table of AND operation looks like:

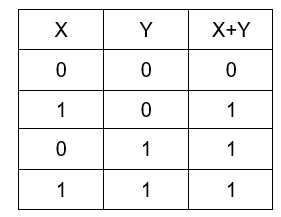
OR: It is a binary operation which gives the output if any of the variables is TRUE (1). The table of OR (+) operation looks like:

NOT: It is a unary operation which inverts the variable. The table of NOT operation looks like:

Now let us consider the given expression,
$Y=\overline{A\text{ }.\text{ }B}$
We can use the similar tables to find the equivalent expression.

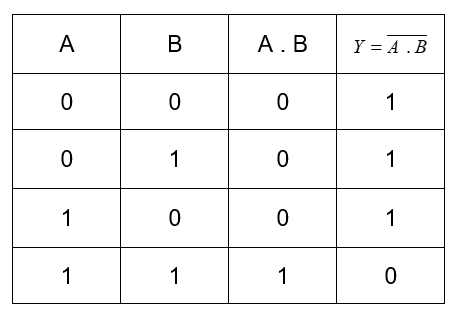
When we look at the basic gates, we can release that the table of $Y=\overline{A\text{ }.\text{ }B}$ is the NOT operation on the AND operation.
The table of NAND operation can be derived from AND table as:

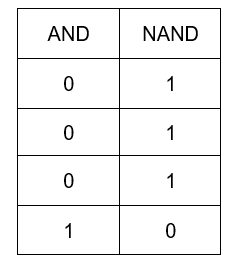
Therefore, the equivalent gate for $Y=\overline{A\text{ }.\text{ }B}$ is a NAND gate.

The correct solution is option A.

Note:
Using the de Morgan’s theorem for Boolean algebra, $Y=\overline{A\text{ }.\text{ }B}$ can be written as $\overline{A\text{ }.\text{ }B}=\overline{A}+\overline{B}$. We can find the solution to the question by using this theorem also. We need to find the complement values of A and B separately and use the OR operator.
All the operations in Boolean algebra can be derived from each other.