Question

n small balls, each of mass m impact elastically each second on a surface with velocity u, then the force experienced by the surface in one second will be
A. 4mnu
B. 2mnu
C. 1.5mnu
D. 0.8mnu

Answer 1

Hint: Calculate the change in momentum of one ball when it hits the surface. Use the formula force i.e. $F=\dfrac{\Delta p}{t}$ to find the force exerted by the surface on the ball. Then use Newton’s third law of motion to find the force exerted by the ball on the surface. At last, multiply this force by n to find the net force.

Formula used:
p=mv
$F=\dfrac{\Delta p}{t}$

Complete step by step answer:
Dealing with all the n balls at once may be difficult. Therefore, let first the case for a single ball.
We know that when a ball of mass m traveling with a velocity u, hits a surface (say a wall) perpendicularly, there is a collision between the wall and the ball. As a result, the wall exerts a force on the ball and its momentum changes. Thus, the ball appears to be bouncing back from the surface of the wall.
The direction of force exerted by the surface on the ball is perpendicular to the surface. Therefore, there is change in the horizontal momentum of the ball. Since, the collision is elastic, the magnitude of the momentum after the collision is equal to magnitude of its momentum before collision (i.e. p=mu). However, the direction of its momentum is opposite to the direction of its momentum before collision, as shown in the figure below.

Before collision:

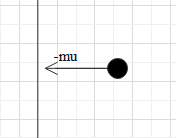
After collision:

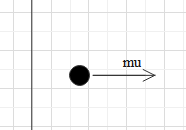
This means that the initial momentum (${{p}_{i}}$) is –mu and the final momentum (${{p}_{f}}$) is mu. Hence, the change in momentum is $\Delta p={{p}_{f}}-{{p}_{i}}=mu-(-mu)=2mu$
Force is equal to the change in momentum of the ball divided by the time taken for the change.
i.e. $F=\dfrac{\Delta p}{t}$
Here, it is given that the collision is for 1 second and the change in momentum is 2mu.
$\Rightarrow F=\dfrac{2mu}{1}=2mu$.
Therefore, the wall exerts a force equal to 2mu.
Now, according to Newton’s third law of motion, the wall will exert a force on the ball and the ball will also exert a force of equal magnitude on the wall.
This means that the ball exerts a force on the wall, whose magnitude is 2mu.
Let us assume that all the n balls travel horizontally and do not collide with each other. Then in one second, each ball will exert a force of magnitude 2mu on the wall and the net force will be n times the force exerted by one ball.
i.e. ${{F}_{net}}=2mnu$
Hence, the correct option is B.

Note: Although we found the answer for the given question, we have neglected many factors of the motion of the balls. It is assumed that there is no gravity. If we consider the gravity, the balls will not move with constant velocity before and after collision.
It is also assumed that the balls do not collide with each other. If they collide, then the situation will be different.