Question
Question: N similar slabs of the cubical shape of edge b are lying on the ground. The density of the material ...
N similar slabs of the cubical shape of edge b are lying on the ground. The density of the material of the slab is ρ. Work done to arrange them one over the other is
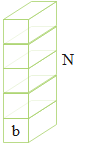
Explanation
Solution
The work done to arrange the cubical shaped slabs equals the work done by the external force and the gravitational force. This gravitational force equals the change in the potential energy, which in turn equals the work done by the external force.
Formula used:
& \rho =\dfrac{m}{V} \\\ & V={{b}^{3}} \\\ & \Delta U={{U}_{f}}-{{U}_{i}} \\\ \end{aligned}$$ **Complete step-by-step answer:** From the given information, we have the data as follows. The number of similar slabs of cubical shape is, N. The edge of each cubical shaped slab is, b. The density of the material of the slab is, $$\rho $$. Therefore, the density in terms of volume and the mass is given as follows. $$\begin{aligned} & \rho =\dfrac{m}{V} \\\ & \Rightarrow m=\rho V \\\ \end{aligned}$$ Therefore, the mass of each cube is, m The volume of each cube is, $$V={{b}^{3}}$$. Therefore, the mass of each cube is, $$m=\rho {{b}^{3}}$$. The work done to arrange the cubical shaped slabs one upon the other is equal to the work done by all force. This force equals the change in kinetic energy $$(\Delta k)$$. 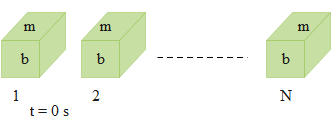 The work will be done by an external agent and the gravitational force (ignoring the frictional force) $$({{W}_{e}}+{{W}_{g}})$$. And, the work is done in such a way that, the change in the kinetic energy remains the same, thus, the final kinetic energy equals zero $$({{K}_{f}}-{{K}_{i}})=0$$. Therefore, the sum of the work done by the external agent and the gravitational force equals zero. $$({{W}_{e}}+{{W}_{g}})=0$$…… (1) The gravitational field is nothing but the conservative field, which equals the change in the potential energy. $$\begin{aligned} & {{W}_{g}}=-\left( {{U}_{f}}-{{U}_{i}} \right) \\\ & \Rightarrow {{W}_{g}}=-\Delta U \\\ \end{aligned}$$ Now substitute this value in the equation (1). $$\begin{aligned} & {{W}_{e}}+\left( -\Delta U \right)=0 \\\ & \Rightarrow {{W}_{e}}-\Delta U=0 \\\ & \therefore {{W}_{e}}=\Delta U \\\ \end{aligned}$$ **Therefore, the work done equals the change in the potential energy.** 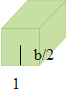 When the cubical shaped slabs were lying on the floor, the initial potential energy was, $$\begin{aligned} & {{U}_{i}}=mg\left( \dfrac{b}{2} \right)+mg\left( \dfrac{b}{2} \right)+........mg\left( \dfrac{b}{2} \right) \\\ & \Rightarrow {{U}_{i}}=Nmg\left( \dfrac{b}{2} \right) \\\ \end{aligned}$$ Substitute the expression of the mass of slab in the above equation. $$\begin{aligned} & {{U}_{i}}=N\left( \rho {{b}^{3}} \right)g\left( \dfrac{b}{2} \right) \\\ & \Rightarrow {{U}_{i}}=N\rho g\left( \dfrac{{{b}^{4}}}{2} \right) \\\ \end{aligned}$$ Therefore, the initial potential energy of the “N” cubical shaped blocks is, $${{U}_{i}}=N\rho g\left( \dfrac{{{b}^{4}}}{2} \right)$$. Now, we will compute the value of the final potential energy of the slabs. $$\begin{aligned} & {{U}_{f}}=mg\left( \dfrac{b}{2} \right)+mg\left( b+\dfrac{b}{2} \right)+mg\left( 2b+\dfrac{b}{2} \right)+.......mg\left( \left( N-1 \right)b+\dfrac{b}{2} \right) \\\ & \Rightarrow {{U}_{f}}=mg\left[ \dfrac{b}{2}+\dfrac{3b}{2}+\dfrac{5b}{2}+.....\left( N-\dfrac{1}{2} \right)\dfrac{b}{2} \right] \\\ \end{aligned}$$ Continue the further computation. $$\begin{aligned} & {{U}_{f}}=mgb\left[ \dfrac{1}{2}+\dfrac{3}{2}+\dfrac{5}{2}+.....+\dfrac{2N-1}{2} \right] \\\ & \Rightarrow {{U}_{f}}=mg\dfrac{b}{2}\times \dfrac{N}{2}(1+2N-1) \\\ & \Rightarrow {{U}_{f}}=\dfrac{mgbN}{4}(2N) \\\ & \therefore {{U}_{f}}=\dfrac{mgb{{N}^{2}}}{2} \\\ \end{aligned}$$ Now, substitute the expression of the mass in the above equation. $$\begin{aligned} & {{U}_{f}}=\dfrac{\left( \rho {{b}^{3}} \right)gb{{N}^{2}}}{2} \\\ & \Rightarrow {{U}_{f}}=\dfrac{\rho g{{b}^{4}}{{N}^{2}}}{2} \\\ \end{aligned}$$ Therefore, the final potential energy of the “N” cubical shaped blocks is, $${{U}_{f}}=\dfrac{\rho g{{b}^{4}}{{N}^{2}}}{2}$$. Now, using the values of the initial and the final potential energies, we will compute the change in the potential energy which equals the work done to arrange the slabs one over the other. $$\begin{aligned} & \Delta U={{U}_{f}}-{{U}_{i}} \\\ & \Rightarrow \Delta U=\dfrac{\rho g{{b}^{4}}{{N}^{2}}}{2}-\dfrac{N\rho g{{b}^{4}}}{2} \\\ & \therefore \Delta U=\dfrac{\rho g{{b}^{4}}({{N}^{2}}-N)}{2} \\\ \end{aligned}$$ Therefore, the work done to arrange the slabs one over the other is, $${{W}_{e}}=\dfrac{1}{2}({{N}^{2}}-N)\rho g{{b}^{4}}$$ $$\therefore $$The value of the work done to arrange the slabs one over the other, is $$\dfrac{1}{2}({{N}^{2}}-N)\rho g{{b}^{4}}$$ **So, the correct answer is “Option C”.** **Note:** The change in the values of the kinetic energy and the potential energies while moving the objects should be known to solve this type of problem.