Question
Question: ‘n’ moles of ideal gas undergo a process \[A\to B\] as shown in the figure. The maximum temperature ...
‘n’ moles of ideal gas undergo a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
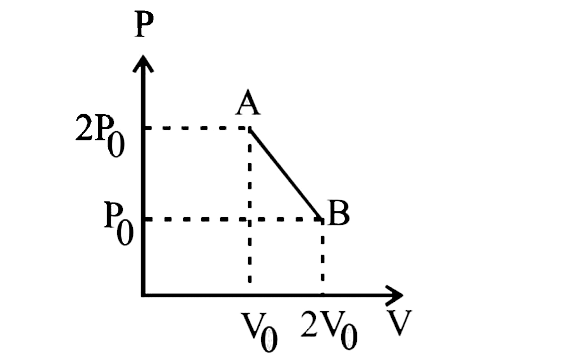
A. 4nR9P0V0
B. 2nR3P0V0
C.2nR9P0V0
D. nR9P0V0
Solution
Two points of the P-V graph have been given. Two-point form of a line can be used to find the formula of the P-V line of the process. We also know from the ideal gas equation that the temperature of the gas is related to pressure and volume as given below. We also know that the for the temperature to be maximum dVdT=0
Formula used:
T=nRPV
Complete answer:
We have been given the pressure vs volume graph. The P-V graph of the given process is a straight line as can be seen from the diagram. Two point of the graph, \left( {{V}_{0}},2{{P}_{0}} \right)$$$$(2{{V}_{0}},{{P}_{0}}) are also given.
So, the equation of the P-V graph in two-point form would be
