Solveeit Logo
Login

Question

Question: \(n\)moles of an ideal gas undergoes a process \(A \to B\) is shown in figure. The maximum temperatu...

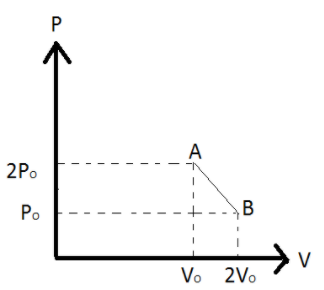
nnmoles of an ideal gas undergoes a process A→BA \to B is shown in figure. The maximum temperature of gas during the process will be
A. 9PoVonR\dfrac{{9{P_o}{V_o}}}{{nR}}
B. 9PoVo4nR\dfrac{{9{P_o}{V_o}}}{{4nR}}
C. 3PoVo2nR\dfrac{{3{P_o}{V_o}}}{{2nR}}
D. 9PoVo2nR\dfrac{{9{P_o}{V_o}}}{{2nR}}

Explanation

Solution

In the given question we have to find the temperature of a gas in an ongoing reaction. We will find it by solving the equation of line. An ideal gas is a hypothetical gas which is composed of many randomly moving point particles that are not subject to interparticle interactions.

Formula used:
Equation of line: Y−Y1=Y2−Y1X2−X1(X−X1)Y - {Y_1} = \dfrac{{{Y_2} - {Y_1}}}{{{X_2} - {X_1}}}(X - {X_1})
Ideal gas equation PV=nRTPV = nRT

Complete step by step solution:
From the given diagram the maximum temperature will be TT and the product of it will be maximum.
From the equation of line we have;
Y−Y1=Y2−Y1X2−X1(X−X1)Y - {Y_1} = \dfrac{{{Y_2} - {Y_1}}}{{{X_2} - {X_1}}}(X - {X_1})
Where
Y:P Y1:P∘ Y2:2P∘ X:V X1:2V∘ X2:V∘Y:P \\\ {Y_1}:{P_ \circ } \\\ {Y_2}:2{P_ \circ } \\\ X:V \\\ {X_1}:2{V_ \circ } \\\ {X_2}:{V_ \circ }
By putting values, we get;
⇒P−P∘=2P∘−P∘V∘−2V∘(V−2V∘)\Rightarrow P - {P_ \circ } = \dfrac{{2{P_ \circ } - {P_ \circ }}}{{{V_ \circ } - 2{V_ \circ }}}(V - 2{V_ \circ })
⇒P−P∘=−P∘V∘(V−2V∘)\Rightarrow P - {P_ \circ } = \dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}\left( {V - 2{V_ \circ }} \right)
⇒P=−P∘V∘V+3P∘\Rightarrow P = \dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}V + 3{P_ \circ }
⇒PV=−P∘V∘V2+3P∘V\Rightarrow PV = \dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}{V_2} + 3{P_ \circ }V
According to ideal gas equation PV=nRTPV = nRT , therefore
⇒nRT=−P∘V∘V2+3P∘V\Rightarrow nRT = \dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}{V_2} + 3{P_ \circ }V
⇒T=1nR[−P∘V∘V2+3P∘V]\Rightarrow T = \dfrac{1}{{nR}}\left[ {\dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}{V_2} + 3{P_ \circ }V} \right]
For maximum temperature ∂T∂V=0\dfrac{{\partial T}}{{\partial V}} = 0
So, −P∘V∘(2V)+3P∘=0\dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}(2V) + 3{P_ \circ } = 0
⇒−P∘V∘(2V)=−3P∘\Rightarrow \dfrac{{ - {P_ \circ }}}{{{V_ \circ }}}(2V) = - 3{P_ \circ }
⇒V=32V∘\Rightarrow V = \dfrac{3}{2}V_\circ This is the condition for the maximum temperature.
So, the maximum temperature of the gas during the process
Tmax=1nR(−P∘V∘×94V2∘+3P∘×32V∘)T_max = \dfrac{1}{{nR}}\left( {\dfrac{{ - {P_ \circ }}}{{{V_ \circ }}} \times \dfrac{9}{4}V{2_ \circ } + 3{P_ \circ } \times \dfrac{3}{2}{V_ \circ }} \right)
=1nR(−94P∘V∘+92P∘V∘)=94P∘V∘nR= \dfrac{1}{{nR}}\left( { - \dfrac{9}{4}{P_ \circ }{V_ \circ } + \dfrac{9}{2}{P_ \circ }{V_ \circ }} \right) = \dfrac{9}{4}\dfrac{{{P_ \circ }{V_ \circ }}}{{nR}}

**Hence, the maximum temperature of gas during the process is option D. 94P∘V∘nR\dfrac{9}{4}\dfrac{{{P_ \circ }{V_ \circ }}}{{nR}} .

Additional information:**
The ideal gas law was made by combining the gas law and Avogadro law. The gas law states that the pressure of a gas is inversely proportional to volume and directly proportional to temperature whereas Avogadro's Law states that volume or pressure is directly proportional to the number of moles of gas.

Note:
The temperature of a gas is a measure of the average translational kinetic energy of the molecules in a process. The ideal gas equation relates with all the components like the pressure, volume, temperature, and also number of moles of an ideal gas. When we have to find the temperature of a particular line then one has to use the line equation formula.