Question
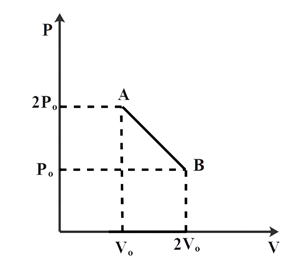
Question: n moles of an ideal gas undergoes a process A and B as shown in the figure. The maximum temperature ...
n moles of an ideal gas undergoes a process A and B as shown in the figure. The maximum temperature of the gas during the process will be:
A. 49nRpoVo
B. 29nRpoVo
C. nR9poVo
D. n=CvCp
Solution
In this question we have been asked to calculate the maximum temperature of gas during the given process. We have been given a pressure vs volume diagram and the number of moles is given as n. We know that the ideal gas equation deals with the relation between the pressure, volume, number of moles, gas constant and temperature. Therefore, we shall use the ideal gas equation to calculate the maximum temperature for a given process.
Formula used:
pV=nRT
y−y1=x2−x1y2−y1(x−x1)
Where,
X and Y are the coordinates
Complete Step by step solution:
It is given that the number of moles is to be taken as n.
Now, from the diagram we can say that equation of line AB is,
y−y1=x2−x1y2−y1(x−x1)
Now, substitute the x and y coordinates from the given diagram
We get,
p−po=Vo−2Vo2po−po(V−2Vo)
On solving,
p−po=Vo−po(V−2Vo)
Therefore,
p=Vo−poV+3po
Now, multiplying both sides by V
We get,
pV=Vo−poV2+3poV
Now, we know from ideal gas equation,
pV=nRT
Therefore, we can write,
nRT=Vo−poV2+3poV
Now, solving for temperature
We get,
T=nR1(Vo−poV2+3poV) ………………… (1)
Now, we know that for the temperature to be maximum,
∂V∂T=0
After substituting value of T
We get,
Vo−po(2V)+3po=0
On solving,
V=23Vo ……………….. (2)
Now, from (1) and (2)
We get,
Tmax=nR1(Vo−po×49Vo2+3po×23Vo)
On solving,
Tmax=nR1(−49poVo+29poVo)
Therefore,
Tmax=49nRpoVo
Therefore, the correct answer is option A.
Note:
The ideal gas equation is an equation defining a hypothetical ideal gas. The normal gases can never be as accurate as the ideal gas. The ideal gas has certain limitations and it is based on the assumption that the gas taken into account is ideal or a perfect gas. Ideal gas equation can be derived from kinetic theory of gases. The state of a gas is determined by pressure, volume and temperature. The ideal gas relates these parameters with each other.
