Question
Question: \(n\) moles of an ideal gas undergoes a process \(A \to B\) as shown in the figure. The maximum temp...
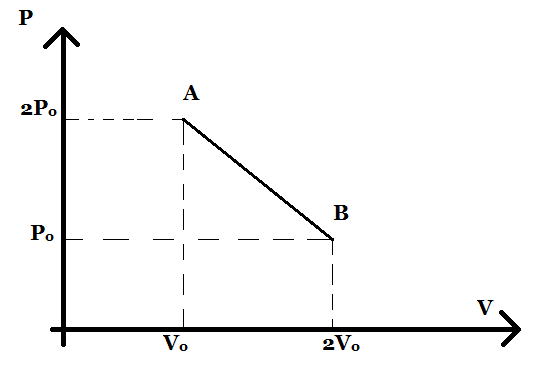
n moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
A. 4nR9P0V0
B. 2nR9P0V0
C. nR9P0V0
Solution
Here we shall obtain the equation of the given straight line in the graph using the two-point formula of a straight line equation. We shall substitute this equation in the ideal gas equation to eliminate either the pressure P, or the volume V to obtain an equation having temperature and another variable (here volume). To maximize the temperature we shall differentiate the equation.
Formula used: PV=nRT
Complete step by step answer:
From the graph given above, we can find the equation of the straight line using a two-point formula. The equation of the line is
V−V0P−2P0=V0−2V02P0−P0.
⇒V−V0P−2P0=−V0P0
Upon rearranging the equation we get,
⇒P=−V0P0(V−V0)+2P0
⇒P=−VV0P0+3P0
Now from the ideal gas equation, we get
PV=nRT
where P is the pressure of the gas, V is the volume of the gas, n is the number of moles of the ideal gas, R is the real gas constant, and T is the absolute temperature.
Substituting the equation of pressure P, as obtained previously into this ideal gas equation, we have,
(−VV0P0+3P0)V=nRT.
Thus we have obtained an equation of the temperature T in terms of a single variable V, the volume of the ideal gas. Thus to maximize the temperature, over the entire process A→B, we have to differentiate the above equation with respect to the volume V.
Thus, from (−VV0P0+3P0)V=nRT, we have
dVd(−VV0P0+3P0)V=nRdVdT
⇒(−VV0P0+3P0)+V(−V0P0)=nRdVdT
Upon simplifying we get,
⇒nRdVdT=−2VV0P0+3P0
Since we are maximizing the temperature T over the volume V within the process, we will have dVdT as 0, since the temperature will reach its peak value, which we need to obtain.
Thus substituting dVdT=0, in the above equation, we have,
⇒nR(0)=−2VV0P0+3P0
⇒0=−2VV0P0+3P0
On simplifying and rearranging, we get,
⇒2VV0P0=3P0
⇒V=23V0
We also check that this value is within the limits of the process, i.e. within A and B.
Substituting this value of V in the equation of the straight line, we have the pressure value as,
⇒P=−(23V0)V0P0+3P0
⇒P=23P0
We also check that this value is within the limits of the process, i.e. within A and B.
Thus now substituting both these values of pressure and temperature in the ideal gas equation, we have
PV=nRT
⇒(23P0)(23V0)=nRTmax
where Tmax is the maximum temperature which is attained at the substituted values of pressure and volume.
⇒Tmax=(23P0)(23V0)nr1
⇒Tmax=4nR9P0V0
Thus, the correct answer is option (A).
Note: On differentiating the equation of temperature and volume, we obtained an equation where we have substituted dVdT=0. This happens at both the maxima and minima of the temperature. To check whether the point is really a maxima, we have to obtain dV2d2T and which we get equal to −nR2VV0P0. Since this value is negative, thus the concerned temperature is the maximum.
