Question
Question: \('n'\) moles of an ideal gas undergoes a process \(A \to B\) as shown in the figure. The maximum te...
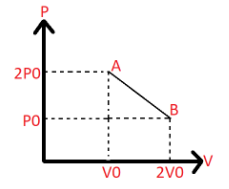
′n′ moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
A. 2nR3P0V0
B. 2nR9P0V0
C. nR9P0V0
D. 4nR9P0V0
Solution
After establishing a relationship between the two variables of pressure and volume using the equation of a straight line pertaining to the graph, we will equate it with the ideal gas equation. Using the boundary conditions for maximum temperature, we will be able to determine the maximum temperature.
Formulae used:
Equation of a straight line: (x−x0)=y2−y1x2−x1(y−y0)
Where y,y1,y2 and x,x1,x2 are the y and x intercepts of a graph.
Ideal gas equation: PV=nRT
Where P is the pressure of the gas and is expressed in Bars (B), V is the volume of the gas and is expressed in meter cube (m3), n is the number of moles of the gas, R is the universal gas constant and T is the temperature of the gas and is expressed in Celsius (∘C).
Complete step by step answer:
From the graph we have the following data:
At A:
Pressure =2P0
Volume =V0
At B:
Pressure =P0
Volume =2V0
To establish a relationship between the two, we will use the equation of a line for the given graph.
We know that, (y−y0)=x2−x1y2−y1(x−x0).
Substituting the intercepts according to our graph we get,
(V−V0)=P2−P1V2−V1(P−P0)
According to the graph, V2=2V0,V1=V0,P2=P0,P1=2P0. Substituting the same we get,
(V−V0)=P0−2P02V0−V0(P−P0)
Simplifying the above equation we get,
Now, we know that for an ideal gas PV=nRT
Rearranging this we get,
P=VnRT
Substituting the above in the relationship established between volume and pressure we get,
VnRT=V0−P0(V−3V0)
Upon rearrangement to arrive at an expression for temperature T we get,
T=nRV0−P0(V2−3V0V)
We need to determine the value of V.
Now, we know that at maximum temperature, rate of change of temperature with respect to volume of an ideal gas is constant. That is dVdT=0.
Therefore, differentiating the expression for temperature with respect to volume we get,
dVdT=dVd(nRV0−P0(V2−3V0V))
Upon simplification and substitution of boundary condition dVdT=0 we will establish a relationship between volume and pressure only,
dVdT=dVd(nRV0−P0(V2−3V0V)) ⇒0=dVd(nRV0−P0(V2−3V0V)) ⇒0=V0−P0(V2−3V0V) ⇒3P0=V0P02V ⇒2V−3V0=0 ⇒V=23V0
Substituting this value in the equation for temperature we get,
T=nRV0−P0(V2−3V0V) ⇒T=nRV0−P0(49V02−29V02) ⇒T=nRV0−P04−9V02 ∴T=4nR9P0V0
Therefore, The maximum temperature of the gas during the process will be 4nR9P0V0.
Hence, the correct option is D.
Note: All assumptions are made considering the gas in question as an ideal gas. For real gases equations and relations become more complex and difficult to calculate. Therefore assuming gas to be an ideal gas is the easiest way to solve the question.
