Question

$n$ identical cubes each of mass $m$ and edge $L$ are lying on a floor. If the cubes are to be arranged as one over the other in a vertical stack, the work to be done is:
$A)\text{ }\dfrac{Lmng\left( n-1 \right)}{2}$
$B)\text{ }\dfrac{Lg\left( n-1 \right)}{mn}$
$C)\text{ }\dfrac{\left( n-1 \right)}{Lmng}$
$D)\text{ }\dfrac{Lmng}{2\left( n-1 \right)}$

Answer 1

We can solve this problem by finding out the initial potential energy of all the blocks and the final potential energy of the blocks when kept in a vertical stack. The difference in these two potential energies will give the value of the work done.

Formula used:
$U=mgh$

Complete step-by-step answer:
We will find the change in the potential energy of the system of all the blocks. This change in potential energy will be equal to the work done for the process of stacking the blocks.
The potential energy $U$ of a body of mass $m$ at a height $h$ above some reference point is given as
$U=mgh$ --(1)
Where $g$ is the acceleration due to gravity.
Now, let us analyze the question.
At first, $n$ cubes of mass $m$ and edge length $L$ is kept on the floor.
We will consider the system to be the set of all these blocks.
We will consider the ground as the reference point in this question.
The centre of mass of a block will be at its centre.
The height of the centre of mass above the ground will be nothing but half of the edge length as will be clear from the below figure.

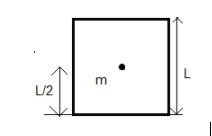
Using (1) the initial potential energy of each block will be
$mg\dfrac{L}{2}$
The initial potential energy ${{U}_{i}}$ of the system will be the sum of the potential energies of $n$ blocks
$\therefore {{U}_{i}}=nmg\dfrac{L}{2}$ --(2)
Now, the blocks are stacked one by one vertically.
The height of the centre of mass from the ground of the ${{p}^{th}}$ block in the vertical stack will be (the first one is considered to be the lowest one)
$\left( 2p-1 \right)\dfrac{L}{2}$ --(3)
Using (1), the final potential energy of this block will be
$mg\left( 2p-1 \right)\dfrac{L}{2}$
The final potential energy ${{U}_{f}}$ of the system will be the sum of the potential energies of all the blocks.
$\Rightarrow {{U}_{f}}=\sum\limits_{p=1}^{n}{mg\left( 2p-1 \right)\dfrac{L}{2}}$
$\Rightarrow {{U}_{f}}=\dfrac{mgL}{2}\sum\limits_{p=1}^{n}{2p-1}$
$\Rightarrow {{U}_{f}}=\dfrac{mgL}{2}\left[ \sum\limits_{p=1}^{n}{2p-\sum\limits_{p=1}^{n}{1}} \right]$
$\Rightarrow {{U}_{f}}=\dfrac{mgL}{2}\left[ 2\left( n\left( \dfrac{n+1}{2} \right) \right)-n \right]=\dfrac{mgL}{2}\left[ n\left( n+1 \right)-n \right]=\dfrac{mgL}{2}{{n}^{2}}$ $\left( \because \sum\limits_{x=1}^{n}{x}=x\left( \dfrac{x+1}{2} \right),\sum\limits_{x=1}^{n}{1}=n \right)$
--(4)
Therefore, the change in potential energy of the system is
$\Delta U={{U}_{f}}-{{U}_{i}}$
Using (2) and (4) in the above equation, we get
$\Delta U={{n}^{2}}mg\dfrac{L}{2}-nmg\dfrac{L}{2}=nmg\dfrac{L}{2}\left( n-1 \right)=\dfrac{Lmng\left( n-1 \right)}{2}$
This is the amount of external work required as the external work done is used up for changing the potential energy of the system.
Therefore, the required work done is $\dfrac{Lmng\left( n-1 \right)}{2}$.

So, the correct answer is “Option A”.

Note: Students often make the mistake and forget that in the final case, the potential energy of each block will be different and dependent upon the height of the centre of mass above the ground which is obviously different for each block in the vertical stack. They may think that the potential energy of the system is the product of the number of blocks and the potential energy of the block corresponding to the top. This will lead to a completely wrong answer for the final potential energy and hence wrong value for the work done.