Question
Question: $4 \sin \frac{2\pi}{7} - \tan \frac{\pi}{7} = \sqrt{7}$. ...
4sin72π−tan7π=7.
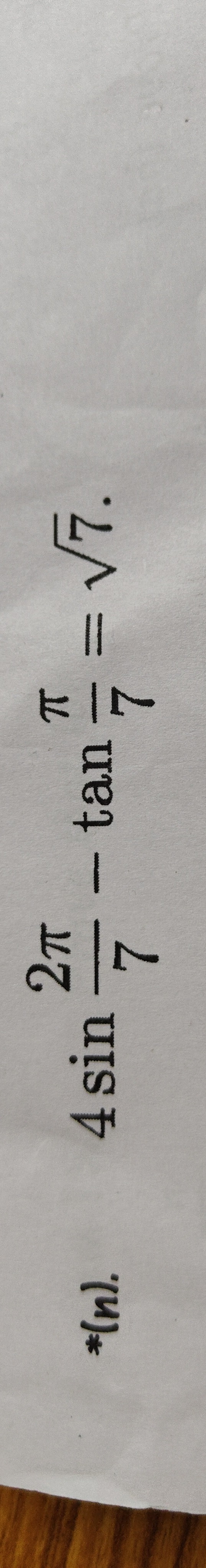
True
Solution
To verify the identity 4sin72π−tan7π=7, we will use a known trigonometric identity related to angles of the form nkπ.
Key Identities for n=7:
-
The product of sines: ∏k=1n−1sinnkπ=2n−1n. For n=7: sin7πsin72πsin73πsin74πsin75πsin76π=27−17=647. Since sin(π−x)=sinx, we have: sin74π=sin(π−73π)=sin73π sin75π=sin(π−72π)=sin72π sin76π=sin(π−7π)=sin7π So, the product becomes: (sin7πsin72πsin73π)2=647 Taking the square root (all sines are positive for angles in (0,π)): sin7πsin72πsin73π=87. (Equation 1)
-
The product of cosines: ∏k=1n−1cosnkπ=2n−1sin(nπ/2) for odd n. For n=7: cos7πcos72πcos73πcos74πcos75πcos76π=27−1sin(7π/2)=64sin(3π+π/2)=64−sin(π/2)=−641. Since cos(π−x)=−cosx, we have: cos74π=cos(π−73π)=−cos73π cos75π=cos(π−72π)=−cos72π cos76π=cos(π−7π)=−cos7π So, the product becomes: (cos7πcos72πcos73π)(−cos73π)(−cos72π)(−cos7π)=−641 −(cos7πcos72πcos73π)2=−641 (cos7πcos72πcos73π)2=641 Taking the square root (all cosines are positive for angles in (0,π/2), here 7π,72π,73π are all in (0,π/2)): cos7πcos72πcos73π=81. (Equation 2)
Deriving the Tangent Product Identity: Divide Equation 1 by Equation 2: cos7πcos72πcos73πsin7πsin72πsin73π=1/87/8 tan7πtan72πtan73π=7. (Equation 3)
Verifying the Given Identity: Let A=7π. The identity to verify is 4sin2A−tanA=7. Substitute 7 from Equation 3 into the identity: 4sin2A−tanA=tanAtan2Atan3A Rearrange the terms: 4sin2A=tanA+tanAtan2Atan3A 4sin2A=tanA(1+tan2Atan3A) Express tangents in terms of sines and cosines: 4sin2A=cosAsinA(1+cos2Acos3Asin2Asin3A) 4sin2A=cosAsinA(cos2Acos3Acos2Acos3A+sin2Asin3A) Use the cosine difference formula: cosXcosY+sinXsinY=cos(X−Y). 4sin2A=cosAsinAcos2Acos3Acos(3A−2A) 4sin2A=cosAsinAcos2Acos3AcosA Cancel cosA: 4sin2A=cos2Acos3AsinA Multiply both sides by cos2Acos3A: 4sin2Acos2Acos3A=sinA Use the double angle formula 2sinXcosX=sin2X: 2(2sin2Acos2A)cos3A=sinA 2sin4Acos3A=sinA Use the product-to-sum formula 2sinXcosY=sin(X+Y)+sin(X−Y): sin(4A+3A)+sin(4A−3A)=sinA sin7A+sinA=sinA Subtract sinA from both sides: sin7A=0 Since A=7π, we have 7A=7×7π=π. sinπ=0. This is a true statement. Therefore, the original identity is correct.
