Question

In the arrangement shown, the value of M for which slipping is just about to start between the blocks is (g = 10 m/s²) (String and pulley are ideal)

(μ = 0.4) Smooth

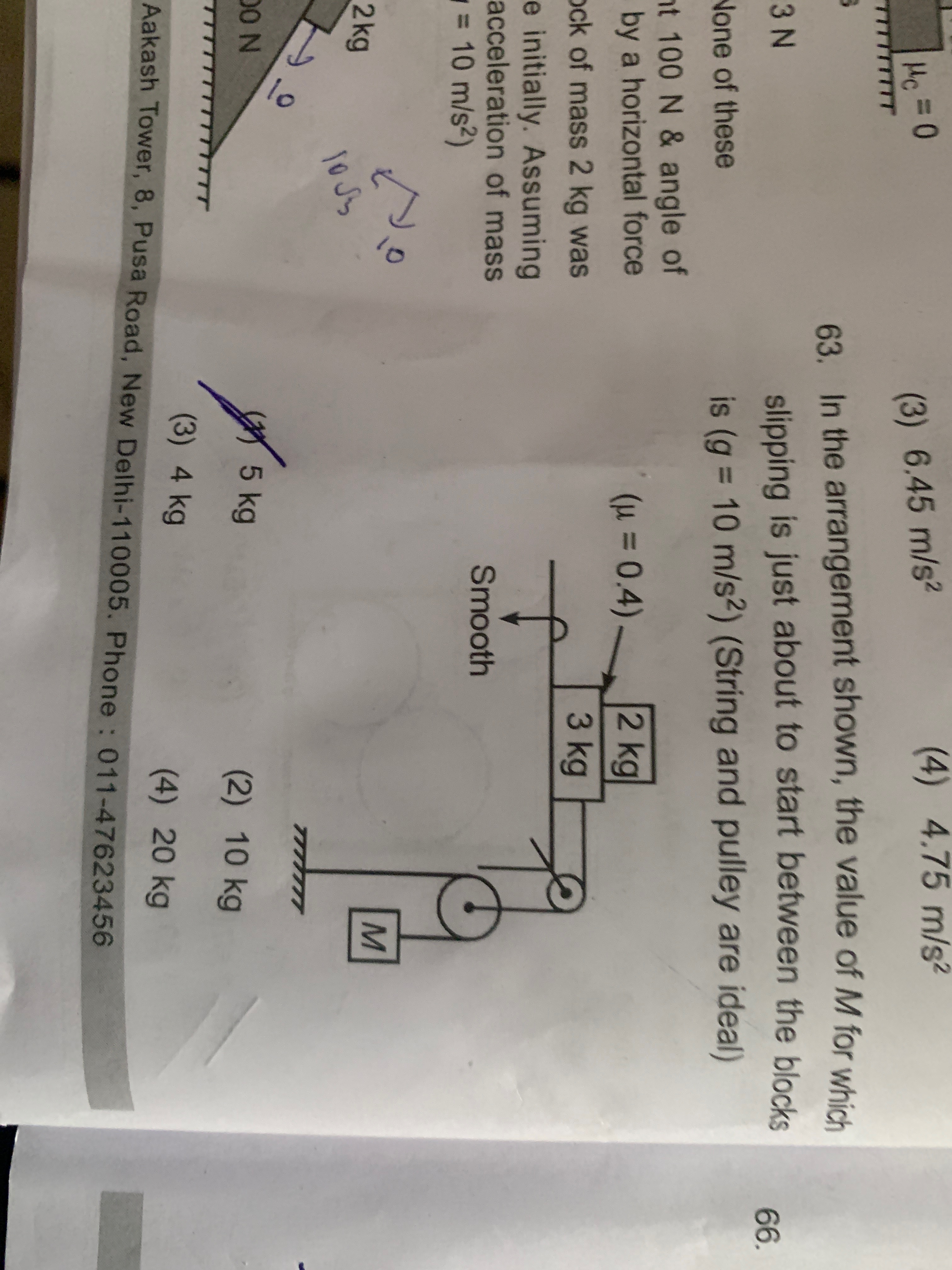
• A. 5 kg
• B. 10 kg
• C. 4 kg
• D. 20 kg

Answer 1

M = 10/3 kg ≈ 3.33 kg. (None of the given options is correct)

Answer 2

We wish to choose the mass M (hanging from an ideal pulley attached to the 3‐kg block on a frictionless table) so that a 2‐kg block resting on top of the 3‐kg one is “just on the point” of slipping. (The friction coefficient at the 2–3 contact is μ = 0.4.) A standard way to treat such “no–slip” problems is to first “glue” the two blocks so that they accelerate together at a common acceleration a; then the friction force needed on the 2‐kg block is that force which “pulls” it along. In what follows we take g = 10 m/s².

Let

m₁ = 2 kg (top block),

m₂ = 3 kg (bottom block),

and let M be the hanging mass.

Because the only horizontal force acting on the top block is the friction f from the 3‐kg block, we have

(1)  f = m₁·a.

For the interface the “no–slip” condition is maintained as long as the static friction does not exceed its maximum value

(2)  f_max = μ·(normal on m₁) = μ·(m₁g) = 0.4×(2×10) = 8 N.

Thus, for the “just–no–slip” case the top block must be accelerated with

a = f_max/m₁ = 8/2 = 4 m/s².

Next, write the equations for the 3‐kg block and the hanging mass. (Remember that the only horizontal forces on the 3–kg block are the tension in the string and the reaction friction from the top block.) For the 3‐kg block the net force is

(3)  T – f = m₂·a     (with f = 8 N and a = 4 m/s²)

so that

T = m₂·a + 8 = 3×4 + 8 = 12 + 8 = 20 N.

For the hanging mass M the equation (taking its downward acceleration as a) is

(4)  M·g – T = M·a  →  T = M·(g – a).

Equate the two expressions for T:

M·(10 – 4) = 20  →  6M = 20  →  M = 20/6 = 10/3 kg ≈ 3.33 kg.

Thus the mass which “just keeps” the two blocks together (i.e. at the verge of slipping) is M = 10/3 kg.

Looking at the given options:

(1) 5 kg  (2) 10 kg  (3) 4 kg  (4) 20 kg

None of these is equal to 10/3 kg (≈3.33 kg). (Sometimes an approximate answer may be “rounded up” but here even the closest option, 4 kg, is a significantly higher mass.) Hence the correct answer is not among the given choices.

Core Explanation (minimal):

1. For the top (2‐kg) block the friction f is the only horizontal force so f = 2a. With f_max = 0.4·(2·10)=8 N, the maximum acceleration before slip is a = 8/2 = 4 m/s².
2. For the 3‐kg block: T – 8 = 3×4 = 12, so T = 20 N.
3. For the hanging mass M: 10M – T = M×4 → 10M – 20 = 4M → 6M = 20 → M = 10/3 kg ≈ 3.33 kg.
4. None of the provided options (5, 10, 4, 20 kg) matches 10/3 kg.