Question

Mr. Verma $\left( 50kg \right)$ and Mr. Mathur$\left( 60kg \right)$ are sitting at the two extremes of a $4m$ long boat $\left( 40kg \right)$ standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process.
(A). $\dfrac{40}{3}cm$
(B). $\dfrac{50}{3}cm$
(C).$\dfrac{110}{3}cm$
(D). $\dfrac{30}{10}cm$

Answer 1

When no external force acts on a system, the center of mass of the system remains constant. This problem can be solved using the concept that since there are no external forces on the system, the center of mass of the system will remain the same. By equating the centers of mass for the initial and final conditions we can find the shift in the position of the boat.

Formula used:
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$
where ${{r}_{x}}$ and ${{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass $m$ with respect to $\left( x,y \right)$.

Complete step-by-step answer:
In this problem, since all the men are assumed to be equal in height and movement of the boat is only allowed in the horizontal plane, the center of mass in the vertical direction is not of required importance in solving the question.
We will consider the two men along with the boat to be the system.
Hence, we will solve this problem only in one dimension (the horizontal) to make it easier.
Let us draw a diagram.

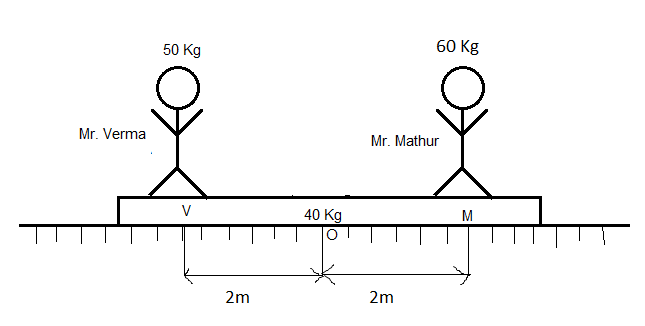
Hence, let O be the origin and the direction towards M (right) be considered the positive axis. Let Mr. Mathur and Mr. Verma be represented as M and V respectively and their masses be ${{M}_{M}}$ and ${{M}_{V}}$ respectively.
The boat can be considered to be a point mass with all its mass concentrated at its center of mass (which will be the origin as it is the mid - point as the center of mass of a symmetric body is at its center).
Now, position of M with respect to O =$2m$ --(1)
Mass of M is given to be ${{M}_{M}}=60Kg$ --(2)
Now, position of V with respect to O =$-2m$ --(3)
Mass of V is given to be ${{M}_{V}}=50Kg$ --(4)
Position of point mass of boat with respect to O =$0m$--(5)
Mass of boat is given to be ${{M}_{Boat}}=40Kg$ --(6)
Now, we will find the center of mass w.r.t point O.
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$ --(7)
where ${{r}_{x}}$ and ${{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass m with respect to $\left( x,y \right)$.
Hence, using (1),(2),(3),(4),(5),(6), (7), we get the center of mass in the horizontal direction $\left( {{P}_{1}} \right)$ as
${{P}_{1}}=\dfrac{\left( {{M}_{V}}\times \left( -2 \right) \right)+\left( {{M}_{M}}\times \left( 2 \right) \right)+\left( {{M}_{Plank}}\times \left( 0 \right) \right)}{{{M}_{V}}+{{M}_{M}}+{{M}_{Plank}}}$
$\therefore {{P}_{1}}=\dfrac{\left( 50\times \left( -2 \right) \right)+\left( 60\times \left( 2 \right) \right)+\left( 40\times \left( 0 \right) \right)}{50+60+40}=\dfrac{-100+120+0}{150}=\dfrac{20}{150}=\dfrac{2}{15}m$ --(8)
Hence, the center of mass of the system is at a distance of $\dfrac{2}{15}m$ from O towards M.
Now, it is given in the question that V and M come to the middle of the boat. Hence, the center of mass relative to point O will also change. Hence, let due to this, the plank shifts horizontally to the right by x. Hence,
Now, position of V with respect to earlier position of O, i.e. origin =$\left( x \right)m$ -(9)
Mass of V is given to be ${{M}_{V}}=50Kg$ --(10)
Now, position of M with respect to earlier position of O, i.e. origin =$\left( x \right)m$ --(11)
Mass of M is given to be ${{M}_{M}}=60Kg$ --(12)
Position of point mass of boat with respect to earlier position of B =$\left( x \right)m$--(13)
Mass of plank is given to be ${{M}_{Plank}}=40Kg$ --(14)
Again using (7),(9),(10),(11),(12),(13),(14), we will get the new center of mass of the system $\left( {{P}_{2}} \right)$as:
${{P}_{2}}=\dfrac{\left( {{M}_{V}}\times \left( x \right) \right)+\left( {{M}_{M}}\times \left( x \right) \right)+\left( {{M}_{Boat}}\times \left( x \right) \right)}{{{M}_{V}}+{{M}_{M}}+{{M}_{Boat}}}$
$\therefore {{P}_{2}}=\dfrac{\left( 50\times \left( x \right) \right)+\left( 60\times \left( x \right) \right)+\left( 40\times \left( x \right) \right)}{50+60+40}$
$\therefore {{P}_{2}}=\dfrac{50x+60x+40x}{50+60+40}=\dfrac{150x}{150}=xm$ -(15)
Now, since there are no external forces on the system but the change has occurred due to internal actions (Mr. Verma and Mr. Mathur coming together in the middle of the system), the center of mass in the initial and final state must remain the same with respect to the origin.
Hence, using (8) and (15),
$x=\dfrac{2}{15}m=\dfrac{200}{15}cm=\dfrac{40}{3}cm$ $\left( \because 1m=100cm \right)$
Hence, the boat moves a distance of $\dfrac{40}{3}cm$ towards the right.
Therefore, the correct option is A) $\dfrac{40}{3}cm$.

Note: Students can make a very common silly mistake of not considering the mass of the boat in the problem since it does not hit the mind at the first sight of the question intuitively. Students may quite easily forget about the mass of the plank and proceed only using the masses of the two men for finding out the center of mass.
However, this leads to a completely wrong result and a lot of wastage of time. Students should be careful of such intricacies in such problems specially.