Solveeit Logo
Login

Question

Question: Mr. A, B and C are trying to put a heavy piston into a cylinder at a mechanical workshop in a railwa...

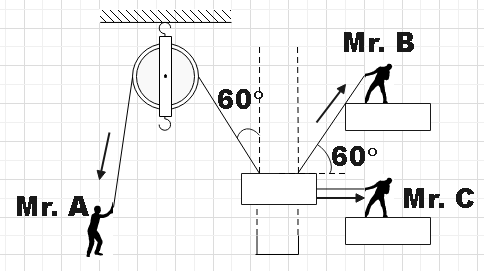
Mr. A, B and C are trying to put a heavy piston into a cylinder at a mechanical workshop in a railway yard. If they apply forcesF1{{F}_{1}}, F2{{F}_{2}} and F3{{F}_{3}} respectively on ropes then for which set of forces at that instant, they will be able to perform the said job?

A. 3F1=F2+2F3\sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}
B. 2F1=F2+F32{{F}_{1}}={{F}_{2}}+{{F}_{3}}
C. 2F2=3F1−F322{{F}_{2}}=\sqrt{3}{{F}_{1}}-\dfrac{{{F}_{3}}}{2}
D. F3=2F1−3F2{{F}_{3}}=2{{F}_{1}}-\sqrt{3}{{F}_{2}}

Explanation

Solution

As a first step, you could go for making a free body diagram for piston marking all the possible forces that are acting on it. You could resolve these forces into their components as per requirement. Then, you could find a condition that will assure the three men completing their task. And thus find the answer.

Complete answer:
In the question we are given three men who are at a mechanical workshop trying to put a heavy piston into a cylinder. The forces applied by Mr. A, Mr. B and Mr. C are given asF1{{F}_{1}}, F2{{F}_{2}} and F3{{F}_{3}} respectively and their directions are as indicated in the diagram. Now let us make a free body diagram and then resolve all the three forces into their respective components.

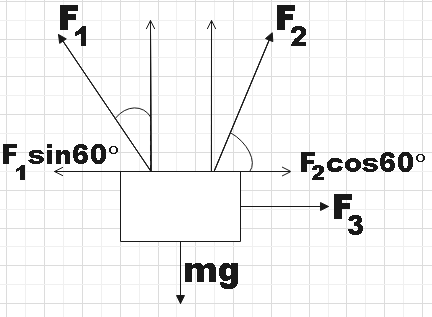
We know that this piston is undergoing only vertical displacement due to all the forces on it and thus we could conclude that the net force in the horizontal direction is zero. Mathematically,
F1sin⁡60∘−F2cos⁡60∘−F3=0{{F}_{1}}\sin 60{}^\circ -{{F}_{2}}\cos 60{}^\circ -{{F}_{3}}=0
⇒3F12−F22−F3=0\Rightarrow \dfrac{\sqrt{3}{{F}_{1}}}{2}-\dfrac{{{F}_{2}}}{2}-{{F}_{3}}=0
⇒3F1−F2−2F3=0\Rightarrow \sqrt{3}{{F}_{1}}-{{F}_{2}}-2{{F}_{3}}=0
∴3F1=F2+2F3\therefore \sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}
So, we have found the condition that ensures that three men will be able to do their job to be,
3F1=F2+2F3\sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}

Hence, option A is found to be the correct answer.

Note:
You may have noted that the free body diagram is made by giving importance to the horizontal forces acting on the piston. We do have vertical components for the forces and the weight of the body acting downwards. However the net displacement of the piston is obviously downwards and as said in the solution, there is no horizontal displacement.